How many calories should i burn in one day. Daily Calorie Requirements: A Comprehensive Guide to Energy Balance
How many calories should you burn in a day. What factors influence your daily calorie needs. How to calculate your resting metabolic rate. Why food quality matters for weight management. How to determine optimal calorie intake for different body types and goals.
Understanding Calorie Balance and Energy Expenditure
Determining the optimal number of calories to consume or burn daily is a complex process that depends on various factors. Energy balance plays a crucial role in weight management, as explained by the National Institutes of Health. When calorie intake exceeds expenditure, weight gain occurs. Conversely, burning more calories than consumed leads to weight loss. Maintaining a balance between intake and expenditure results in weight maintenance.
But how do you calculate your daily energy expenditure? Let’s break down the key components:
- Resting Metabolic Rate (RMR)
- Physical Activity Level
- Non-Exercise Activity Thermogenesis (NEAT)
- Thermic Effect of Food (TEF)
Resting Metabolic Rate (RMR)
RMR represents the energy your body uses at rest to maintain basic bodily functions. The Harris-Benedict equation is commonly used to estimate RMR based on height, weight, age, and gender. For instance, a 40-year-old woman weighing 120 pounds and standing 5’3″ tall has an estimated RMR of 1,286 calories.

Physical Activity Level
Your daily activities and exercise significantly impact your calorie expenditure. Modern technology, such as step counters on smartphones or fitness watches, can help estimate energy expenditure based on activity levels. Additionally, specific exercises burn varying amounts of calories depending on intensity and duration.
Non-Exercise Activity Thermogenesis (NEAT)
NEAT refers to the energy expended for everything we do that isn’t sleeping, eating, or sports-like exercise. This includes activities like cleaning, carrying groceries, or fidgeting. While these activities may seem insignificant, they can contribute substantially to your daily calorie burn.
Thermic Effect of Food (TEF)
TEF is the energy required to digest, absorb, and metabolize the nutrients in the food you eat. It typically accounts for about 10% of your total daily energy expenditure.
Calculating Daily Calorie Needs for Different Body Types
While general guidelines exist, calorie needs vary significantly based on individual factors. Let’s explore how to estimate calorie requirements for different body types and goals:

Calorie Needs for a 120-Pound Woman
A 120-pound woman’s calorie needs depend on her fitness goals and energy expenditure. Using online calculators like MyPlate can provide a rough estimate. These tools consider factors such as age, height, weight, gender, and activity level to suggest daily calorie intake based on whether the goal is weight loss, gain, or maintenance.
Calorie Needs for a 6-Foot Tall Man
For a 6-foot tall man, calorie requirements can vary widely based on weight, muscle mass, activity level, and goals. Generally, taller individuals require more calories due to higher RMR. However, it’s essential to consider individual factors rather than relying solely on height-based estimates.
The Role of Food Quality in Calorie Management
While calorie balance is crucial for weight management, the quality of food consumed plays a significant role in overall health and weight loss success. How does food quality impact your calorie management efforts?
- Nutrient Density: Foods high in nutrients but lower in calories can help you feel fuller while consuming fewer total calories.
- Fiber Content: High-fiber foods slow digestion, promoting satiety and potentially reducing overall calorie intake.
- Blood Sugar Regulation: Foods with a lower glycemic index help maintain stable blood sugar levels, reducing cravings and overeating.
An April 2017 study published in the FASEB Journal demonstrated that increasing fiber intake by 10 grams per day aided in weight loss. This underscores the importance of focusing not just on calorie quantity but also on the types of food consumed.

Strategies for Effective Calorie Management
Managing your calorie intake effectively requires a balanced approach. Here are some strategies to consider:
- Gradual Calorie Reduction: If weight loss is your goal, aim to reduce your calorie intake gradually, starting with a 300-500 calorie daily deficit.
- Regular Monitoring: Track your food intake and weight to assess progress and make necessary adjustments.
- Balanced Nutrient Intake: Ensure your diet includes adequate protein, healthy fats, and complex carbohydrates to support overall health and satiety.
- Increased Physical Activity: Combine dietary changes with regular exercise to create a calorie deficit and improve overall health.
- Mindful Eating: Pay attention to hunger and fullness cues to avoid overeating.
The Impact of Drastic Calorie Reduction
Is severely restricting calories an effective strategy for weight loss? While it may seem logical that dramatically cutting calories would lead to rapid weight loss, this approach can have negative consequences:

- Metabolic Slowdown: Severe calorie restriction can cause your metabolism to slow down, making weight loss more difficult over time.
- Nutrient Deficiencies: Drastically reducing calorie intake can lead to inadequate nutrient consumption, potentially causing health issues.
- Muscle Loss: Without proper nutrition, your body may break down muscle tissue for energy, which can further slow metabolism.
- Hormonal Imbalances: Extreme calorie restriction can disrupt hormone levels, affecting everything from mood to reproductive health.
Instead of drastic measures, focus on creating a moderate calorie deficit through a combination of diet and exercise for sustainable, healthy weight loss.
Tailoring Calorie Intake to Specific Goals
Your calorie needs will vary depending on whether you’re aiming to lose weight, gain muscle, or maintain your current weight. How can you adjust your calorie intake to meet these different goals?
Weight Loss
To lose weight, you need to create a calorie deficit. This can be achieved by:
- Reducing calorie intake by 300-500 calories per day
- Increasing physical activity to burn more calories
- Combining both approaches for more significant results
Remember, a safe and sustainable rate of weight loss is about 1-2 pounds per week.
Muscle Gain
Building muscle requires a calorie surplus along with adequate protein intake and strength training. Consider:
- Increasing calorie intake by 300-500 calories per day
- Consuming 1.6-2.2 grams of protein per kilogram of body weight
- Engaging in regular resistance training
Monitor your progress and adjust your calorie intake to ensure you’re gaining primarily muscle, not excessive fat.
Weight Maintenance
Once you’ve reached your goal weight, maintaining it requires balancing calorie intake with expenditure. This might involve:
- Gradually increasing calories if you’ve been in a deficit
- Continuing to monitor your weight and body composition
- Adjusting your diet and exercise routine as needed to maintain balance
Remember that your maintenance calorie needs may change over time due to factors like age, muscle mass, and activity level.
The Role of Macronutrients in Calorie Management
While total calorie intake is crucial for weight management, the balance of macronutrients (proteins, carbohydrates, and fats) in your diet can significantly impact your results and overall health. How do different macronutrients affect your calorie management efforts?

Protein
Protein plays a vital role in weight management and body composition:
- It has a high thermic effect, meaning your body burns more calories digesting protein compared to carbs or fats
- Protein promotes satiety, helping you feel full and satisfied with fewer calories
- It supports muscle maintenance and growth, which can boost metabolism
Aim for 1.6-2.2 grams of protein per kilogram of body weight, especially if you’re active or trying to lose weight.
Carbohydrates
Carbohydrates are your body’s primary energy source, but the type and amount of carbs you consume can impact your calorie management:
- Complex carbs (like whole grains and vegetables) provide sustained energy and promote satiety
- Simple carbs (like sugar) can lead to energy spikes and crashes, potentially increasing hunger
- Fiber-rich carbs can aid in weight management by promoting fullness and supporting digestive health
The ideal carbohydrate intake varies based on individual factors and goals, but generally, aim for high-quality, nutrient-dense carb sources.

Fats
Despite being calorie-dense, fats play crucial roles in health and can aid in calorie management:
- Healthy fats (like those found in avocados, nuts, and olive oil) promote satiety
- They support hormone production and nutrient absorption
- Including adequate healthy fats in your diet can improve adherence to a calorie-controlled eating plan
Aim for 20-35% of your total calories from healthy fat sources, adjusting based on your individual needs and preferences.
Practical Tips for Implementing Calorie Management
Implementing effective calorie management strategies can be challenging. Here are some practical tips to help you succeed:
- Use a Food Diary: Tracking your food intake can increase awareness and help identify areas for improvement.
- Measure Portions: Use measuring tools or learn to estimate portion sizes accurately to avoid unintentional overeating.
- Plan Meals in Advance: Meal planning can help ensure you’re meeting your calorie and nutrient needs while avoiding impulsive food choices.
- Stay Hydrated: Sometimes thirst can be mistaken for hunger. Drink water regularly throughout the day.
- Incorporate Volume Eating: Focus on low-calorie, high-volume foods like vegetables to feel full on fewer calories.
- Practice Mindful Eating: Pay attention to your food, eat slowly, and listen to your body’s hunger and fullness cues.
- Allow for Flexibility: Include occasional treats in your plan to prevent feelings of deprivation and improve long-term adherence.
- Regular Exercise: Combine your dietary efforts with regular physical activity for optimal results and overall health benefits.
Remember, sustainable calorie management is about finding an approach that works for your lifestyle and preferences while supporting your health and fitness goals.

How Many Calories Should a 120-Pound Woman Consume Daily?
The number of calories a 120-pound woman should consume daily depends on her fitness goals and energy expenditure.
Image Credit: Plateresca/iStock/GettyImages
Figuring out how much to eat in a day is quite complex. If you’re a 120-pound woman, you can estimate your daily calorie needs by figuring out approximately how many calories you’re burning. Then, you can tailor your energy intake to your fitness goals.
Tip
The number of calories a 120-pound woman should consume daily depends on her fitness goals and energy expenditure.
Whether you want to lose, gain or maintain your body weight, everything depends on energy balance, according to the National Institutes of Health. If you eat more calories than you burn, you’ll gain weight. If you torch more calories than you take in, you’ll lose weight. If those numbers are the same, you’ll maintain your body weight.
Read more: Recommended Caloric Intake for Weight Loss
120-Pound Woman Energy Requirements
The number of calories you burn in a day depends on your metabolism and activity level. Your resting metabolic rate is the amount of energy your body uses at rest. It includes the energy your organs use just to keep your body running. You can calculate this number by using the Harris-Benedict equation.
Your resting metabolic rate is the amount of energy your body uses at rest. It includes the energy your organs use just to keep your body running. You can calculate this number by using the Harris-Benedict equation.
The Harris-Benedict equation is a formula that uses your height, weight, age and gender to estimate your resting metabolic rate. For example, a 40-year-old 120-pound woman who stands 5 feet and 3 inches tall has an estimated resting metabolic rate of 1,286 calories.
Once you’ve calculated your resting metabolic rate, you have to figure out your activity level. You can use a step counter on your phone or watch to monitor your steps for the day. These calculators typically estimate your energy expenditure based on your activity level.
You also have to factor in the number of calories you burn in the gym. Harvard Health Publishing provides the estimated calories burned by activity and body weight.
Based on this data, a 125-pound person would burn 270 calories in 30 minutes on the elliptical, or 300 calories in 30 minutes while running at 6 miles per hour.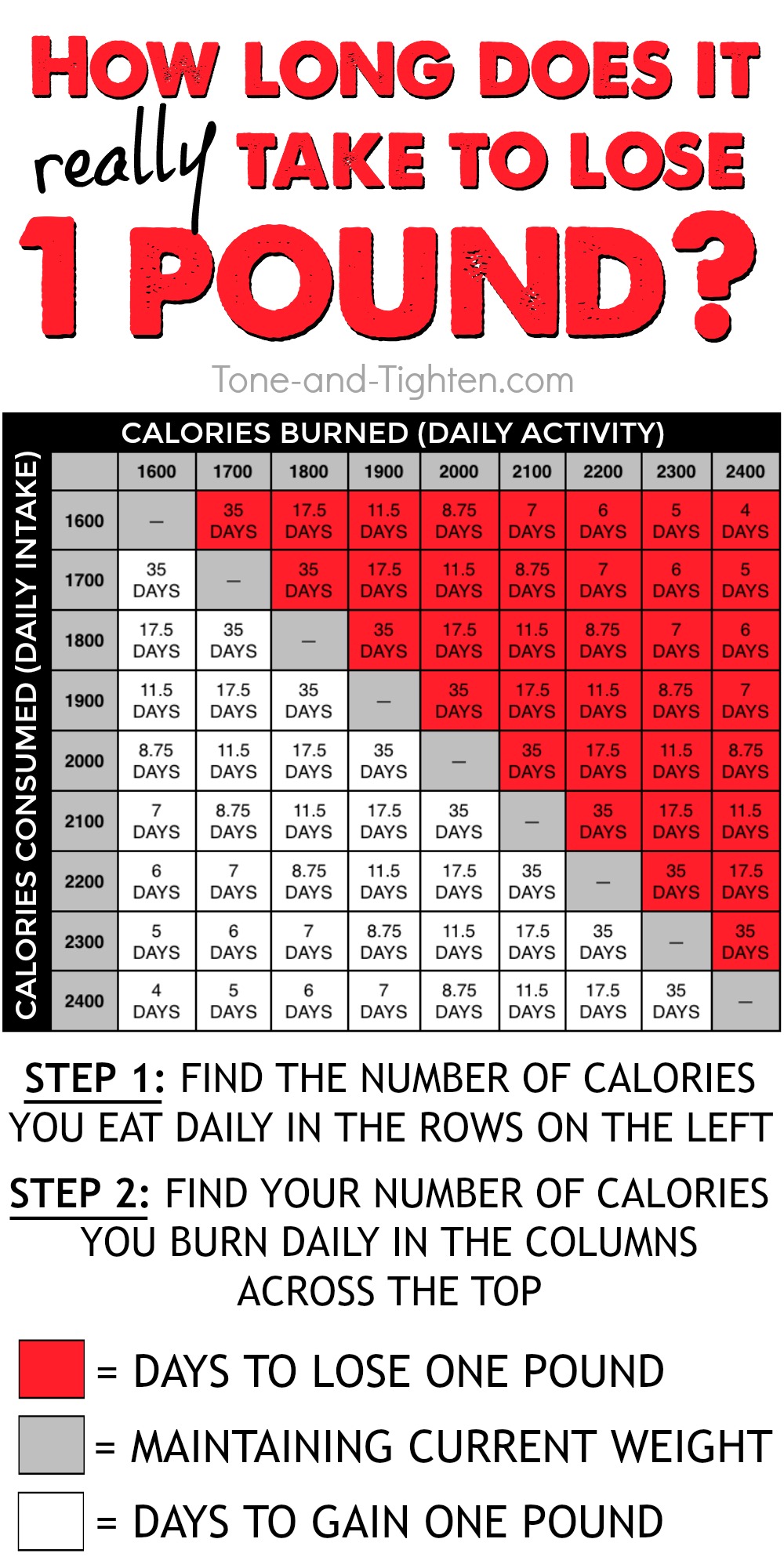 Keep in mind that body weight matters when measuring activity, so a 120-pound girl burns less than a 180-pound one doing the same activity.
Keep in mind that body weight matters when measuring activity, so a 120-pound girl burns less than a 180-pound one doing the same activity.
Another factor that affects your energy expenditure is non-exercise activity thermogenesis. As you go through your day, you do little activities like cleaning the dishes or carrying grocery bags. These activities don’t count as exercise, but they do burn calories. Once you’ve added up all your activity for the day and your resting metabolic rate, you’ll have an idea of how many calories you burn in a day.
To keep things simple, use an online calculator like MyPlate, which will tell you how many calories to consume per day based on your goals. For example, if you are 120 lbs, simply input your goal, height and gender to calculate your ideal energy intake. Keep in mind that all calculators are giving you estimates, so the numbers they provide may not be 100 percent accurate.
Read more: Calories, Weight and Height According to Age
Food Quality Matters
Whether you lose or gain weight comes down to energy balance, but the quality of the food you eat still matters. For example, eating a candy bar versus eating fruits. The sugar in candy bars digests quickly, whereas the fiber from fruits slows down sugar absorption into the bloodstream. Fiber makes you feel fuller, which can ultimately help you eat less and lose weight.
For example, eating a candy bar versus eating fruits. The sugar in candy bars digests quickly, whereas the fiber from fruits slows down sugar absorption into the bloodstream. Fiber makes you feel fuller, which can ultimately help you eat less and lose weight.
An April 2017 study published in the FASEB Journal showed that increasing fiber intake by 10 grams per day helped subjects lose more weight. This shows that what you eat is important, so instead of simply focusing on how many calories you take in, focus instead on the types of food you’re eating.
Keep in mind that drastically reducing your calorie intake can slow your metabolism and lead to nutrient deficiencies, among other side effects. If you decide to lower your calorie intake, it’s better to do so gradually. Start by cutting 300 to 500 calories per day, track your progress and adjust your diet accordingly.
Daily Calories for 6′ Tall Men
The number of daily calories you need depends on your goals, body shape, body size and activity level.
Image Credit: Aamulya/iStock/GettyImages
Determining your daily caloric intake is a complex process that varies from person to person. The calories needed for a 6-foot man might be completely different from another man or woman of the same height.
Tip
The number of daily calories you need depends on your goals, body shape, body size and activity level.
Calories for 6′ Tall Men
Estimating the resting metabolic rate for a 6-foot-tall man is easy with online calculators, but the number isn’t necessarily accurate. The National Academy of Sports Medicine offers a simple calculator that you may use. These online tools typically estimate your resting metabolic rate and energy expenditure, then give you a calorie goal.
Your resting metabolic rate is the number of calories you burn per day at rest. It includes all the energy it takes for you to breathe, for your organs to function and for blood to move through your body. This number accounts for a large portion of the calories you burn in a day.
This number accounts for a large portion of the calories you burn in a day.
Your energy expenditure is generally a rough estimate of the number of calories you burn per day on top of your resting metabolic rate. That number accounts for any workouts you do, as well as simple tasks like cleaning the dishes and walking to or from work.
Read more: Formula for Caloric Intake
Calculating Caloric Requirements
One of the most most widely used formulas to measure resting metabolic rate is the Harris-Benedict equation. It uses your height, weight, age and gender to determine this number.
For example, a 30-year-old man who stands 6′ tall and weighs 200 pounds burns an estimated 2,013 calories per day at rest. Body size and shape play a big role, so you can expect the calorie intake for a 4’11 woman to be different from that for a 6′ tall man.
When you add activity on top of that, the number of calories burned in a day goes up. A table from Harvard Health gives estimates for calories burned during 30 minutes of various activities at three different body weights. For example, a 185-pound man burns 266 calories in 30 minutes of vigorous weight training compared to 400 calories on the elliptical trainer. Estimates like these can give you an idea of how many calories you’re burning from your workout.
A table from Harvard Health gives estimates for calories burned during 30 minutes of various activities at three different body weights. For example, a 185-pound man burns 266 calories in 30 minutes of vigorous weight training compared to 400 calories on the elliptical trainer. Estimates like these can give you an idea of how many calories you’re burning from your workout.
Some step counters also give you an estimate of how many calories you burn from activity based on how far you walk in a given day. You may not realize how little or how much you walk around throughout the day until you actually track it.
The problem with using estimated equations is that there are more variables in determining how many calories you torch daily than just height, weight and age.
For example, fat-free mass, which represents the weight of your ligaments, bones, muscles, tendons and internal organs, is a big factor in the number of calories you burn per day. Since this number isn’t necessarily reflected in height, the differences between two males of the same age, height and weight can be different. One can have more muscle and one can have more fat.
One can have more muscle and one can have more fat.
According to a small 30-person study published in September 2016 in the Journal of the American Academy of Nutrition and Dietetics, the Harris-Benedict equation isn’t completely accurate for individuals because it doesn’t take into account the differences in fat-free mass between people. Those differences can be significant.
Read more: Guidelines for Men’s Daily Calorie Intake
Consider Your Goals
Depending on your goals, your calorie requirements may shift. Once you have a rough estimate of the daily number of calories you burn from your resting metabolism and any activity you do, you can determine how many calories you need to eat to gain or lose weight.
If you’re trying to put on pounds, you need to eat above that number — and vice versa if you want to lose weight. This is called energy balance, and it’s a reliable formula for gaining or losing weight according to a March 2017 study published in Cancer Causes & Control. However, since estimated equations aren’t entirely accurate, you should use another form of measurement to track your progress.
However, since estimated equations aren’t entirely accurate, you should use another form of measurement to track your progress.
You may use a scale or a hand-held body fat measurement device for more accurate measurements. Clothes are also a good way to get feedback on your progress. The way your pants or shirts fit will give you an indication of what direction you’re going, rather than relying on slightly inaccurate calorie formulas.
How to Achieve 1 Pound of Weight Loss
Doing the Math With a BMR Calculator to Make Weight Loss Work for You
To lose a pound, you need to have a good idea of how many calories you burn (use for energy) on an average day. According to the U.S. Department of Health and Human Services, the average adult woman expends roughly 1,600 to 2,400 calories per day, and the average adult man uses 2,000 to 3,000 calories per day. (The average adult woman is 5 feet 4 inches tall and weighs 126 lbs, while the average man is 5 feet 10 inches tall and weighs 154 lbs. ) Yet age, activity level, body size, and body composition all influence how many calories a person burns through each day.
) Yet age, activity level, body size, and body composition all influence how many calories a person burns through each day.
To get a more accurate idea of your daily caloric requirements, you can turn to an online metabolic rate calculator. These determine basal metabolic rate (BMR), which refers to the number of calories that the body burns every day for energy just to maintain basic biological functions. It’s based on your height, weight, age, and biological sex, according to diabetes.co.uk. When multiplied by an activity factor (how much you move in a day), you get your daily metabolic rate, an estimate of how many calories you actually burn in 24 hours — and how many calories you need to eat every day just to keep your weight constant, says Sari Greaves, a registered dietitian nutritionist at LBS Nutrition in East Brunswick, New Jersey, and the author of Cooking Well Healthy Kids. Some BMR calculators allow you to enter your body fat versus lean mass, a percentage that accounts for a large amount of the variations between any two people’s basal metabolic rates. But using such a calculator, while more accurate than calculators that do not take into account your body fat versus lean mass will require that you have a tool like calipers (those fat pinchers your doctor may have used on you in the past) or a smart scale to estimate your body composition.
But using such a calculator, while more accurate than calculators that do not take into account your body fat versus lean mass will require that you have a tool like calipers (those fat pinchers your doctor may have used on you in the past) or a smart scale to estimate your body composition.
Once you know your current daily caloric requirement, you can create your own formula for losing weight. Simply put, as long as you are eating fewer calories than that number, or you increase your daily caloric burn with exercise, you will lose weight, explains Audra Wilson, RD, CSCS, a bariatric dietitian and strength and conditioning specialist at the Northwestern Medicine Metabolic Health and Surgical Weight Loss Center at Delnor Hospital in Geneva, Illinois.
For example, you might eat 500 fewer calories, work off 500 more calories through exercise, or do any combination of the two actions to achieve a deficit of 500 calories. For example, you might choose to eat 250 calories fewer than your daily caloric requirement and then do a workout that burns another 250 calories, she says.
In terms of the 3,500-calorie rule, that would mean that if you achieve that 500-calorie deficit at the end of each day, you would lose 1 lb of fat in seven days. Unfortunately, that equation tends to oversimplify — and overestimate losses, so don’t expect to lose that much that fast.
While the math is complicated, the Pennington Biomedical Research Center in Baton Rouge, Louisiana, one of the top nutrition research centers in the United States, has created a weight loss predictor to help you more closely estimate how much weight you would lose with a given daily calorie deficit. It uses mathematical models based on your age, height, weight, and biological sex, as well as the size of your daily caloric deficit. It also provides an estimate of how many calories you need to maintain your body weight (and likely are consuming right now).
RELATED: 9 Hard Truths About Weight Loss That Can Help You Slim Down
When It Comes to Losing Weight, Easy Does It
The size of your caloric deficit affects how fast you lose weight, with larger deficits leading to faster weight loss.
Yet experts typically agree that losing 2 lbs per week is the healthiest and most sustainable pace of weight loss, Wilson explains. If you are losing more than that in a given week, it is likely that you are significantly cutting into your lean muscle mass. By lowering your metabolic rate, this sets you up to eventually regain all of the weight you lost, and possibly then some. When losing more than a couple of pounds per week, you’re also at a higher risk of not having enough macronutrients (protein, carbohydrates, and fat) or vitamins and minerals in your diet, explains Greaves. That’s not because fast weight loss itself deprives the body of nutrients but because, when cutting calories to a point that such rapid weight loss is possible, overall food, and therefore nutrient intake, can be unhealthily low. A study published in January 2018 in Nutrients analyzed three commercial diet plans designed to result in rapid weight loss, and authors reported that participants experienced deficiencies in nutrients such as vitamin D, B vitamins, vitamin E, selenium, and zinc.
However, even with a conservative caloric deficit of a few hundred calories per day, if you are drastically cutting down on processed foods or carbohydrates, you may quickly lose water weight, Greaves says.
Factoring in Diet and Exercise to Shed Unwanted Pounds
Whatever your weight loss goal may be, losing 1 lb should ideally involve both diet and exercise. Pursuing one without the other is setting yourself up to regain the weight later on.
“Diet and exercise go hand in hand,” Wilson says. “Diet is more impactful for weight loss in the short term and exercise is more beneficial in the long term to maintain weight loss.”
Not to mention, most people find it easier to cut 500 calories from their diet than to burn 500 calories through exercise. But without exercise, a larger portion of any weight lost will be from lean muscle, meaning that as you lose weight, your body-fat percentage could actually decrease. In the long term, reduced levels of muscle lower your body’s metabolic rate, meaning that, over time, your body may actually gain fat, she explains.
One way to help keep yourself on target is to track your food using a journal or app. Many allow for you to keep tabs on both calories consumed and calories expended through exercise and everyday tasks, and according to a study published in May 2019 in JMIR mHealth and uHealth, that can be useful in the management of weight loss.
Again, unfortunately, it’s rare for calorie counters to get things perfect, and they typically overestimate energy expenditure, Wilson says. In fact, some research shows that women, on average, underestimate caloric intake by 25 percent.
And if you don’t weigh or measure every ingredient you eat (which can be a challenging undertaking), you can easily think you are in a large caloric deficit when you’re actually in a surplus, meaning you’re consuming more calories than you’re burning, thus effectively gaining weight, she says.
A study published in May 2017 in the Journal of Personalized Medicine, every fitness tracker studied incorrectly estimated caloric burn by at least 20 percent.
Greaves adds, “I don’t disregard the value of having a tracker. They can keep you accountable and reinforce healthy dietary choices. My advice, however, is to use these trackers as tools. Track for mindfulness, not for calorie counting.”
Small changes in your daily habits, designed to increase your activity and reduce your caloric intake to healthy levels for you, can lead to slow, steady, and lasting weight loss.
RELATED: Smart Health: I Tried Noom for Weight Loss — and It Worked
Diet and Exercise Tips That Help With Weight Loss
These diet and exercise tips can help you create the daily caloric deficit that will help you lose 1 lb:
Eat whole grains. They fill you up and take longer to digest than the simple carbohydrates contained in processed flour or white rice. Choose whole-grain bread, brown rice, and oatmeal. Whole grains also contain lots of healthy fiber, which may further aid weight loss, according to a wealth of research. According to the U.S. Department of Agriculture (USDA), a cup of brown rice offers 3.12 grams (g) of fiber, which provides 11 percent of the daily value of this nutrient.
According to the U.S. Department of Agriculture (USDA), a cup of brown rice offers 3.12 grams (g) of fiber, which provides 11 percent of the daily value of this nutrient.
Think before you drink. Sodas and fruit juices contain tons of calories and added sugar, which can contribute to weight gain and hurt your health in a variety of ways, according to the Harvard T.H. Chan School of Public Health. For example, the USDA notes that 8 ounces of fruit punch contains 110 calories and 26 g of sugar. Simply switching to water (plain or sparkling) can decrease your caloric intake almost effortlessly, she says.
RELATED: Thirsty? Try These 11 Refreshing Alternatives to Soda
Eat regular meals. “Skipping meals can cause dips in your blood sugar and make you more prone to overeating later on in the day,” Greaves says. Stick to three meals and one or two snacks per day. If you’re prone to forgetting or missing meals, set reminders in your phone for all meals and snacks.
Do regular strength training. Muscle at rest burns more calories than fat at rest. Increasing your muscle mass helps you lose weight more efficiently. The more muscle you have, the more calories you will burn, even at rest. What’s more, strength training will help ensure that you are losing the bulk of your weight from fat, rather than muscle, Foster explains. Yes, it’s possible to actively build lean muscle while still losing fat.
Break up your workout. Try to engage in at least 30 minutes of exercise a day, but current federal guidelines show that you don’t have to do it all at once for weight loss benefits. For example, you could take a brisk 10-minute walk around the block in the morning, then do a 20-minute strength-training workout later in the day, Wilson says. This way, even the busiest of people can squeeze in calorie-burning activities. Top-rated app options for tracking activity include MyFitnessPal, Simple Workout Log, and FitNotes.
Now that you know what it takes to lose 1 lb of fat, your weight loss plan will be more effective and you’ll start building the motivation to lose more and more.
Additional reporting by Dennis Thompson Jr.
Counting calories: Get back to weight-loss basics
Counting calories: Get back to weight-loss basics
Weight control really boils down to one thing — calories. See what steps you can take to win the calorie battle.
By Mayo Clinic Staff
Despite all the diet strategies out there, weight management still comes down to the calories you take in versus those you burn off.
Fad diets may promise you that avoiding carbs or eating a mountain of grapefruit is the secret to weight loss, but it really comes down to eating fewer calories than your body is using if you want to shed pounds.
Calories: Fuel for your body
Calories are the energy in food. Your body has a constant demand for energy and uses the calories from food to keep functioning. Energy from calories fuels your every action, from fidgeting to marathon running.
Energy from calories fuels your every action, from fidgeting to marathon running.
Carbohydrates, fats and proteins are the types of nutrients that contain calories and are the main energy sources for your body. Regardless of where they come from, the calories you eat are either converted to physical energy or stored within your body as fat.
These stored calories will remain in your body as fat unless you use them up, either by reducing calorie intake so that your body must draw on reserves for energy, or by increasing physical activity so that you burn more calories.
Tipping the scale
Your weight is a balancing act, but the equation is simple: If you eat more calories than you burn, you gain weight. And if you eat fewer calories and burn more calories through physical activity, you lose weight.
In general, if you cut 500 to 1,000 calories a day from your typical diet, you’ll lose about 1 pound (0.5 kilogram) a week.
It sounds simple. However, it’s more complex because when you lose weight, you usually lose a combination of fat, lean tissue and water. Also, because of changes that occur in the body as a result of weight loss, you may need to decrease calories further to continue weight loss.
Also, because of changes that occur in the body as a result of weight loss, you may need to decrease calories further to continue weight loss.
Cutting calories
Cutting calories requires change but doesn’t have to be difficult. These changes can have a big impact on the number of calories you consume:
- Skipping high-calorie, low-nutrition items
- Swapping high-calorie foods for lower calorie options
- Reducing portion sizes
Saving calories by cutting high-calorie, low-nutrition items
Skipping one or two high-calorie items is a good place to start when cutting calories. For example, you could skip your morning latte, soda at lunch or that bowl of ice cream you always have after dinner.
Think about what you eat and drink each day and identify items you could cut out. If you think that skipping your indulgence will leave you with a craving, try a low-calorie substitution.
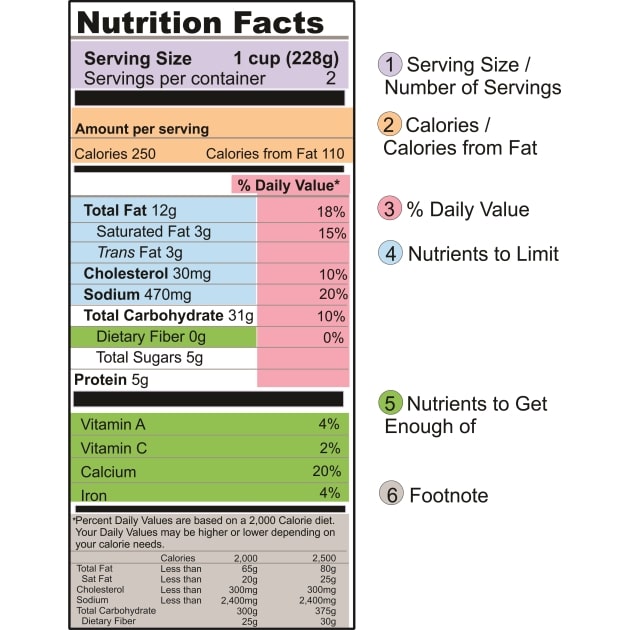
Instead of . .. .. | Calories* | Choose … | Calories* |
|---|---|---|---|
| *Actual calories may vary by brand. | |||
| Flavored latte, 8 oz. (250 g) | 134 | Black coffee, 8 oz. (250 g) | 0 |
| Chocolate ice cream, 1 cup (135 g) | 292 | Strawberries, 1 cup (150 g) | 48 |
| Lemon-lime soda, 16 oz. (491 g) | 201 | Sparkling water, 16 oz. (491 g) | 0 |
Swapping high-calorie foods for lower calorie options
Simple substitutions can make a big difference when it comes to cutting calories. For example, you can save about 60 calories a glass by drinking fat-free milk instead of whole milk. Instead of having a second slice of pizza, reach for some fresh fruit. Snack on air-popped popcorn instead of chips.
Snack on air-popped popcorn instead of chips.
| Instead of … | Calories* | Choose … | Calories* |
|---|---|---|---|
| *Actual calories may vary by brand. | |||
| Whole milk, 1 glass (244 g) | 146 | Skim milk, 1 glass (244 g) | 83 |
| Fast food pepperoni pizza, 2 slices | 626 | Fast food pepperoni pizza, 1 slice, plus grapes, 1 cup (150 g) | 417 |
| Ranch-flavored tortilla chips, snack bag (85 g) | 400 | Air-popped popcorn, 3 cups (24 g) | 92 |
Reducing your portion sizes
The sizes of your portions affect how many calories you’re getting. Twice the amount of food means twice the number of calories.
Twice the amount of food means twice the number of calories.
It’s common to underestimate how much you’re eating, especially if you’re dining out. Controlling your portions is a good way to control calories.
Don’t confuse a serving with a portion. A portion is the amount of food you put on your plate.
| Typical portion | Calories* | Standard serving | Calories* |
|---|---|---|---|
| *Actual calories may vary by brand. | |||
| Orange juice, 8 oz. (248 g) | 120 | Orange juice, 4 oz. (124 g) | 60 |
| Buttermilk pancake, 6-inch diameter (77 g) | 175 | Buttermilk pancake, 4-inch diameter (38 g) | 86 |
| Whole-grain pasta, cooked, 2 cups (280 g) | 414 | Whole-grain pasta, cooked, 1/2 cup (70 g) | 103 |
Try these tips to control portion sizes and cut calories:
- Start small.
 At the beginning of a meal, take slightly less than what you think you’ll eat. If you’re still hungry, eat more vegetables or fruit.
At the beginning of a meal, take slightly less than what you think you’ll eat. If you’re still hungry, eat more vegetables or fruit. - Eat from plates, not packages. Eating directly from a container gives you no sense of how much you’re eating. Seeing food on a plate or in a bowl keeps you aware of how much you’re eating. Consider using a smaller plate or bowl.
- Check food labels. Be sure to check the Nutrition Facts panel for the serving size and number of calories per serving. You may find that the small bag of chips you eat with lunch every day, for example, is two servings, not one, which means twice the calories you thought.
- Use a calorie counter. Check out reputable resources that offer tools to count calories, such as websites or smartphone applications.
Putting it all together
Replacing high-calorie foods with lower calorie alternatives and reducing your portion sizes can help you cut calories and improve weight control. For a successful — and sustainable — weight management plan, you also need to increase your physical activity. Combining regular activity and healthy eating will best help you achieve and maintain a healthy weight.
For a successful — and sustainable — weight management plan, you also need to increase your physical activity. Combining regular activity and healthy eating will best help you achieve and maintain a healthy weight.
Dec. 08, 2020
Show references
- Atallah R, et al. Long-term effects of 4 popular diets on weight loss and cardiovascular risk factors. Circulation Cardiovascular Quality Outcomes. 2014; doi:10.1161/CIRCOUTCOMES.113.000723.
- Balancing diet and activity to lose and maintain weight. U.S. Centers for Disease Control and Prevention. http://www.cdc.gov/healthyweight/calories/. Accessed Dec. 4, 2020.
- Colditz GA. Healthy diet in adults. http://www.uptodate.com/search. Accessed Dec. 4, 2020.
- Hall KD, et al. Quantification of the effect of energy imbalance on bodyweight. Lancet. 2011; doi:10.1016/S0140-6736(11)60812-X.
- 10 tips: Enjoy your food, but eat less. U.S. Department of Agriculture. https://www.choosemyplate.
 gov/ten-tips-enjoy-your-food. Accessed Dec. 4, 2020.
gov/ten-tips-enjoy-your-food. Accessed Dec. 4, 2020. - FoodData Central. U.S. Department of Agriculture, Agricultural Research Service. https://fdc.nal.usda.gov. Accessed Dec. 4, 2020.
- Perreault L. Obesity in adults: Dietary therapy. https://www.uptodate.com/contents/search. Accessed Dec. 4, 2020.
- Hensrud DD, et al. Set your targets. In: The Mayo Clinic Diet. 2nd ed. Mayo Clinic; 2017.
- Duyff RL. Reach and maintain your healthy weight. In: Academy of Nutrition and Dietetics Complete Food and Nutrition Guide. 5th ed. Houghton Mifflin Harcourt; 2017.
See more In-depth
.
How Many Calories Should I Burn a Day to Lose Weight?
If you are trying to lose weight, the first thing you should find out is how many calories you need to burn every day.
Knowing how many calories you burn each day will help you figure out how many calories to consume so that you create a calorie deficit that will lead to weight loss.
Don’t worry, it’s not as complicated as it sounds, our online calorie calculator will do all calculations for you and give you a straight forward answer.
It is highly recommended though to go through our step-by-step example to understand what these numbers mean.
Here is a summary of what we want to achieve:
Steps to calculate how many calories you need to burn a day
- Calculate your Basal Metabolic Rate (BMR). This is how many calories are needed by your body to function properly (based on your age, sex and height)
- Use the Harris-Benedict formula (BMR X activity level) to find out how many calories you need to consume per day to maintain your current weight
- Decide how many pounds you want to lose and when
- Based on the above, calculate how many calories you should save per day either through dieting or by burning calories through exercising
BMR and Calorie Calculator
How to use our calculator: Type your age, select your gender, enter your height in either feet and inches or cm, enter your weight in pounds or kg and select your daily activity level. Enter how much weight you want to lose (in pounds or kg) and the period (in days). Click the CALCULATE button.
Enter how much weight you want to lose (in pounds or kg) and the period (in days). Click the CALCULATE button.
How many calories to burn a day to lose weight?
You can use our calculator above to find out your Basal Metabolic Rate (BMR), how many calories you burn per day based on your activity level and how many calories you need to save per day (through dieting or exercise) in order to reach your weight loss goal.
To understand the theory behind these calculations, read our step by step example below.
You do not have to keep a pen and paper because our daily calorie calculator will do the hard part.
Step 1: Calculate your BMR
The first step is to calculate your Basal Metabolic Rate (BMR).
Many studies have found that in general women need 1500-2000 calories to maintain their current weight and for men the range goes to 2000-2500 calories.
This number is also known as the Basic Metabolic Rate (BMR).
In essence, this figure gives you the number of calories your body needs on a daily basis in order to function properly.
To calculate you BMR (1), use the formulas below (enter your weight in pounds and height in inches).
BMR for Men: 66 + (6.2 x weight) + (12.7 x height) – (6.76 x age)
BMR for Women: 655.1 + (4.35 x weight) + (4.7 x height) – (4.7 x age)
For example, the BMR for a woman age 20, 5 feet height, weighting 140 pounds is: 1447.65 Calories.
Note
This is not how many calories you should consume per day but how many calories your body needs to function without doing anything. It can also be considered as the number of calories you burn a day doing nothing.
Step 2: The Harris-Benedict Formula
The next step is to use the Harris-Benedict formula (2) to calculate how many calories you need per day to maintain your current weight.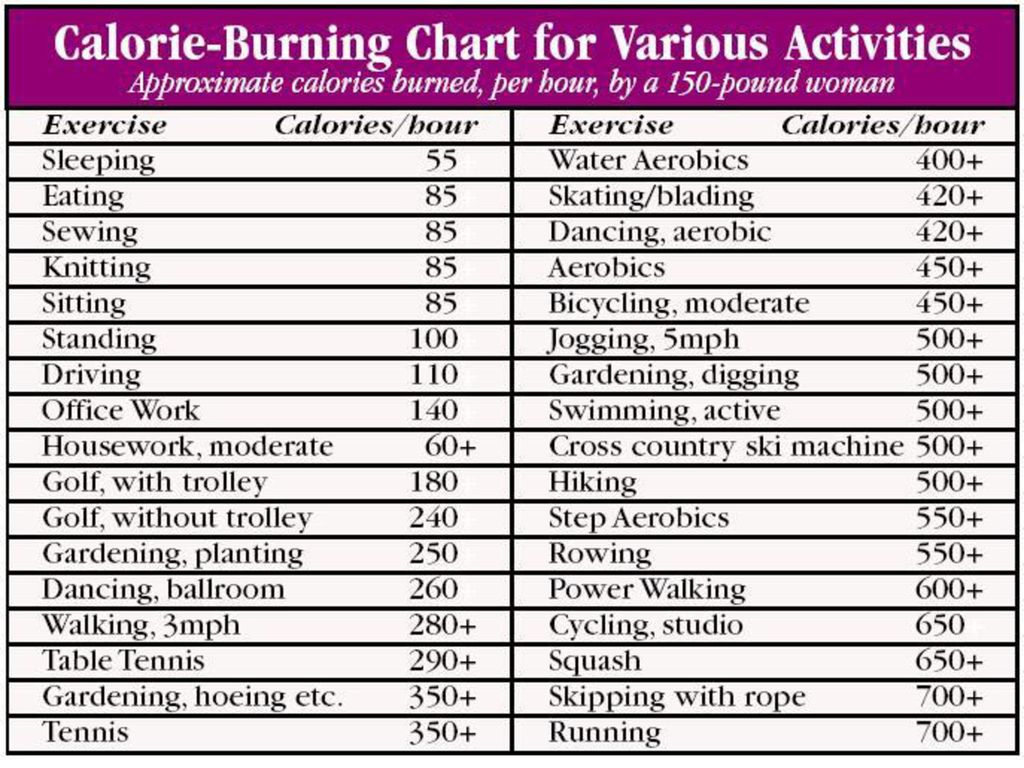
Harris-Benedict Equation = BMR x Activity Factor
| Daily Activity | Activity Factor |
| Sedentary (little or no exercise) | 1.2 |
| Lightly Active (light exercise, doing sports 1-3 days per week) | 1.375 |
| Moderately Active (sports/exercise 3-5 days per week) | 1.55 |
| Very Active (intense sports 6 or 7 days per week) | 1.725 |
| Extra Active (sports and exercise, physical job or hard training) | 1.9 |
For example, if your BMR is 1600 calories and you are lightly active during the day then your daily calorie requirements are: 1600 x 1.375 = 2200 calories per day. 2200 calories are needed so that you maintain your current weight.
If you want to lose weight you should be consuming less than 2200 calories per day and if you want to gain weight you should be consuming more than 2200 calories per day.
Step 3: How many pounds you want to lose?
The next step is to decide how many pounds you want to lose and when. To set-up realistic goals, you should understand when do you lose weight.
When do you lose weight?
There are many factors that affect how much weight you can lose (and when) but in its simplest form weight loss will occur when the calories you burn are more than the calories you consume.
Food and drinks (think diet) are the only sources for calories you consume while exercise, physical activity and other body factors affect the rate you burn calories.
So, if you manage to control these 2 sources and create a calorie deficit you will eventually start losing weight.
How many calories are in a pound?
Let’s add one more parameter to our equation which is 1 pound of fat = 3500 calories aprx.
This means that if you consume 3500 more calories than what you burn in a period of time you will gain one pound but if you manage to burn 3500 more calories than you consume you will lose 1 pound.
Step 4: How many calories to burn per day for weight loss
The last step is to calculate how many calories you need to burn per day in order to reach your goal weight.
Note
This is only an estimate and it is not guaranteed that by following this number you will lose or gain weight.
There are many other factors involved in losing weight and the number of calories you consume is just one of the elements and since it is easy to calculate you can use it as your starting point.
Example
Let’s assume that you are a 40 year old woman, 5 ft and 3 inches tall, 143 pounds weight and lightly active. Your goal is to lose 5 pounds in 2 months.
This is how you calculate the amounts of calories to burn per day:
1. Your BMR is 1385 calories
2. Your daily calorie needs based on your current activity level is 1905 calories.
This means that if you consume 1905 calories per day, you will maintain your current weight. If you eat more than 1905 calories you will eventually gain weight and if you eat less than 1905 calories, you will lose weight.
If you eat more than 1905 calories you will eventually gain weight and if you eat less than 1905 calories, you will lose weight.
3. Your goal is to lose 5 pounds / 2.3 kg in 60 days, which is about 17500 calories (1 pound of fat is 3500 calories).
This means you need to save or burn 17,500 extra calories for the next 60 days.
Doing some basic calculations you can find out that this is equivalent to 280 calories per day. If you manage to save 280 calories per day you will lose 5 pounds in 2 months.
4. Subtract the number of calories you need to save per day (Step 3 above) from your daily calorie needs (step 2 above)
Daily Calorie needs – Calorie savings per day = 1905 – 280 = 1625 calories per day.
This is the number of calories you need to eat per day if you want to lose 5 pounds in 2 months!
The amount of calories you need to burn per day, depends on how much you are consuming.
Remember your goal is to save 280 calories per day over and above what your body needs to function properly.
For example, if you are consuming 1800 calories per day, in order to lose weight you need to consume only 1625 calories per day (as calculated above).
This means that you should burn 175 calories per (1800-1625) day through exercise.
So, in this example:
- The number of calories you burn per day for normal body functioning is 1905.
- If you consume 1800 calories per day then it means you are saving 105 calories per day, but this is not enough to reach your weight loss goal which is to lose 5 pounds in 60 days.
- To reach your goal, you need to burn an additional 175 calories per day (280 – 105) through exercise.
To lose weight faster, you can try reducing your daily calorie intake or increase calories burn through exercise.
How many calories you burn through exercise and other activities?
Burning calories is not easy. Those that are counting calories burned while exercising know that it’s hard work to burn those extra calories.
To give you an idea, here is how many calories you can burn in 30-minute activities. (3)
Calorie Burned in Common Activities and Exercises
Counting calories and weight loss
Does calorie counting works for weight loss?
From my experience a lot of people hesitate to even try and lose weight because they don’t know from where to start. They know that they should go on a diet and exercise regime but the lack of measurable goals creates uncertainty and this leads to failure before to even begin!
To bypass this problem and have clear goals on what you want to achieve, you can start your weight loss process by doing some simple calorie calculations, as explained above.
By calculating how many calories you should be eating per day and how many calories you should be burning per day, you can have a better picture about your daily calorie needs and a rough estimate as to when you will be able to reach your ideal weight.
What you should know when trying to lose weight
- When you start a diet or weight loss program you will not only lose fat. Especially at the beginning you will lose water weight and in some cases you may also lose muscle. So the results in the first few weeks may be misleading.
- When you make sudden or drastic changes to your diet the body will try to adapt by lowering the metabolic rate. In other words it enters a protective mode by reducing the number of calories it needs per day. As a result weight loss may slow down.
- The absolute minimum amount of calories you can consume per day is 1000-1100 kcal. It is not recommended to go beyond this number for any reason.
- The recommended weight to lose per week is between 1 – 1.5 pounds. Anything above that can have other implications to your health and normal body functioning.
- Do not forget that drinks also carry calories so make sure that you include drinks in your daily calorie calculations.

- You can use a technique called “calorie cycling” to make the process easier to follow. This means that once you calculate your daily calorie needs you can go above and below this range on different days of the week. If for example you daily calorie needs are 1700 you can choose to go above this number on Monday and Wednesday and below this number the rest days of the week but try to avoid exaggerations.
- Make sure that you give correct measurements for your weight and height when calculating your BMR.
- Do not lie about your activity level but try to be as accurate as possible.
- Do not decrease your daily calorie intake by more than 500 calories per day. Better expand the time period. Reducing your intake by 500 calories is a lot and very difficult to follow for a long time.
- Always consult your doctor or dietician before making any changes to your diet or exercise routine.
Conclusion
As explained above, you can use these calculations to give you an idea where you stand and how much effort you need to make until you meet your goals and target weight.
Weight loss depends on a lot more factors and calculating the calories you need per day is just your starting point.
Don’t forget that the amount of calories you should burn a day depends on the number of calories you consume through food and the number of calories you want to save for weight loss.
If you eat more calories than you need, you will have to burn more calories through exercise to stay aligned with your weight loss goals.
How to Burn More Calories Than You’re Eating
Burning more calories than you eat in a day is referred to as a “calorie deficit” and is the basis of many weight-loss equations. The idea is daily calories in minus daily calories out = caloric deficit.
The first thing you need to understand is that one pound of fat is made of about 3,500 of extra calories. To lose one pound of fat, you need to create a caloric deficit of 3,500 calories. For example if you wanted to lose one pound a week divide 3,500 calories by seven to get 500; that means negative 500 calories a day overall.
FIND OUT IF WEIGHT-LOSS SURGERY IS RIGHT FOR YOU?
There are only 3 ways you can create a deficit of calories each day:
- Eat fewer calories than you burn each day. Keep in mind that your body burns calories all day long as part of your basal metabolic rate (BMR), because it takes energy (calories) for your body to perform basic functions that are necessary for life—breathing, digesting, circulating, thinking and more. It’s important for you to know what your BMR is so you can estimate how many calories you burn in an average day. In addition to that, you also burn some calories with normal daily activities like bathing, cleaning, walking, typing and exercising (which uses even more calories each day). So by simply taking in less calories each day, that means less excess calories you have to burn off. Easy ways to do this include: eat less fast food or junk food, eat more fresh vegetables and fruits, eat lean protein, reduce the amount of bad fats, and drink more water.

- Burn more calories than you consume by increasing your physical activity. If you eat enough calories to support your BMR, but add more exercise, you’ll create a caloric deficit simply by burning extra calories. This only works if you’re not overeating to begin with. Example: If you exercise more to burn an extra 500 calories each day, you’ll lose about one pound of fat in a week (500 calories x 7 days = 3,500 calories). You can workout more or just add more movement into your daily lifestyle. Some ideas: ride your bike walk rather than driving places, always take the stairs, move around at work rather than sitting a desk, play with your kids or dog, do squats while watching TV. Get creative with your day, the possibilities are endless
- A combination of eating fewer calories and exercising to burn more calories. This is the most effective way to lose weight and keep it off. It’s much easier to create a substantial calorie deficit when you combine eating less with exercise because you don’t have to deprive yourself so much, or exercise in crazy amounts.
 Studies show that the combination of diet and exercise are compounded to increase weight loss more than the equivalent of one method alone. One theory is that the exercise increases metabolism which rev’s the fat burning even more. Example: If you cut 200 calories a day from your diet and burned 300 calories a day by exercising, you’d lose about one pound per week. Compare that to the other examples above—so you’re losing weight at about the same rate without making such extreme changes to your diet or exercise routine.
Studies show that the combination of diet and exercise are compounded to increase weight loss more than the equivalent of one method alone. One theory is that the exercise increases metabolism which rev’s the fat burning even more. Example: If you cut 200 calories a day from your diet and burned 300 calories a day by exercising, you’d lose about one pound per week. Compare that to the other examples above—so you’re losing weight at about the same rate without making such extreme changes to your diet or exercise routine.
The key to any successful weight loss is consistency. Over time your calorie deficit will ‘add up.’ and you will lose the extra weight. But remember to be super accurate with your caloric intake and exercise because after all it is a math equation.”
It’s also important to note that although this seems like simple math, our bodies are actually very complicated. We also have emotions, hormones, stress and more that can factor into the equation so you might not always see the results you expect based on equations alone.
If efforts to lose weight with diet and exercise have been unsuccessful and your body mass index (BMI) is 40 or higher (or 35 or more and you have a serious weight-related health problem, such as type 2 diabetes, high blood pressure or severe sleep apnea), you may qualify for weight-loss surgery. To learn more, visit our weight-loss surgery program page or call us at (310) 836-7000. To find a bariatric surgeon, click here.
How Many Calories Should I Burn During a Workout?
Whether you’re trying to lose weight or you’re simply working out to stay healthy, it can be hard to determine how many calories you need to burn to meet your goals. And even if you know that number, it can seem trickier still to figure out exactly how much time and effort you’ll need to put in to get there. The good news? POPSUGAR spoke with a trainer to help break it down.
How Many Calories Should You Burn During a Workout?
Let’s start with the most straightforward benchmark: if you’re simply trying to maintain your weight, you don’t have to worry as much about your calorie burn. Just aim to exercise for 150 minutes per week, or 30 minutes, five days a week, explained Holly Perkins, BS, CSCS, author of Lift to Get Lean and creator of The Glutes Project. (This is the standard recommendation for heart health.)
Just aim to exercise for 150 minutes per week, or 30 minutes, five days a week, explained Holly Perkins, BS, CSCS, author of Lift to Get Lean and creator of The Glutes Project. (This is the standard recommendation for heart health.)
If your goal is weight loss, you’ll need to track your calories more carefully. “If you’re trying to lose one pound of body fat per week, you need a caloric deficit of 3,500 calories per week,” Holly told POPSUGAR. She suggests still working out five days during the week, with the goal of burning 250 calories per session. You’ll need to reduce your calories by a total of 500 each day to reach a deficit of 3,500, so plan to save 250 calories from your diet on workout days, and 500 calories from your diet on rest days.
How Long Should You Work Out to Lose Weight?
Calorie burn depends on a number of factors, but Holly explained that a woman who weighs between 150 and 160 pounds will burn approximately 500 calories per hour when working out at 80 to 90 percent of her maximum heart rate. Therefore, she suggests putting in 30 to 40 minutes during a cardio session.
Therefore, she suggests putting in 30 to 40 minutes during a cardio session.
You’ll expend fewer calories with strength training, but building lean muscle helps your body burn more calories even at rest, which helps to offset the difference. So, “you should also aim for 30 to 40 minutes during a strength training workout,” Holly said.
Of course, the most accurate way to track your calorie burn is with a heart rate monitor, which can be programmed with stats like your height, age, weight, and BMI. Still, Holly cautioned against getting too wrapped up in the numbers. “Ultimately, if you aren’t losing weight while maintaining this exercise schedule, for the most part it comes down to the fact that you’re eating too many calories,” she said. Working with a registered dietitian can help get you back on track.
90,000 How many calories you need to burn to lose weight
Calorie counting is one of the most famous ways to lose weight. Its essence is simple: you need to spend more energy than you consume. In other words, create a calorie deficit.
Its essence is simple: you need to spend more energy than you consume. In other words, create a calorie deficit.
How many calories you need to burn to lose 5 kg
In 1958, scientist Max Wishnofsky determined that one pound of fat in the human body corresponds to 3,500 kilocalories. Thus, one kilogram of fat is equal to 7,716 kcal.
This means that you need to create a deficit of 7,716 kcal in order to lose 1 kg.
Let’s say your goal is to lose 5 kg. You consume 2,000 kcal per day and spend 2,500 – a 500 kcal deficit is created. If you stick to this diet, you will lose one kilogram in 15 days. And to lose 5 kg, you need 2.5 months.
It looks simple. But when it comes to the processes in our body, everything becomes much more complicated. Our body easily adapts to new conditions, including hunger.
How to whip up a slow metabolism
At first, a calorie deficit will actually lead to rapid weight loss, but then the metabolism will slow down . Under conditions of malnutrition, the body will begin to conserve energy. For intense weight loss, you will need more than your usual diet.
Under conditions of malnutrition, the body will begin to conserve energy. For intense weight loss, you will need more than your usual diet.
For example, playing sports. Strength training and high-intensity interval training create an oxygen demand in the body. Calories are consumed to cover it, both during training and several hours after it.
Exercise is also necessary for another reason: Provided sufficient protein is consumed, it prevents muscle loss.
How to lose fat, not muscle
The goal of losing weight is to get rid of excess body fat. However, along with fat during a calorie deficit, you also lose muscle mass. This is highly undesirable for a beautiful figure.
In May 2008, scientists from the University of Alabama at Birmingham conducted a study on muscle preservation and energy recovery while losing weight .
It has proven that strength training during a low-calorie diet can help maintain strength and muscle.
However, protein is needed to build muscle. If you are doing strength training while dieting, add protein-rich foods to your diet.
Remember:
- You lose one kilogram of weight, creating a deficit of 7,716 kilocalories.
- This works in the early days of the diet, and then the metabolism slows down.
- To keep your metabolism from slowing down and you lose muscle mass, include protein-rich foods in your diet and engage in strength training.
How to Count Calories
You can use websites and apps with ready-made recipes. You only need to accurately observe the proportions and quantities of ingredients.
Edalite.ru
On this site you will find detailed recipes with photos. At the end of each is indicated the calorie content and content of proteins, fats, carbohydrates and dietary fiber.
Edalite.ru →.
NyamNyamra
There are quite a few recipes on the site. There are filters “Low-calorie”, “Fast”, “Simple”.Calories and nutrient composition are listed in a table. If you change the amount of ingredients, you can click on the “Calculate Calorie” button and find out how many calories will be in the dish.
There are filters “Low-calorie”, “Fast”, “Simple”.Calories and nutrient composition are listed in a table. If you change the amount of ingredients, you can click on the “Calculate Calorie” button and find out how many calories will be in the dish.
“NyamNyamra” →
My Healthy Diet
On this site, all products and recipes are analyzed in detail. Calorie content, amount of proteins, fats and carbohydrates are indicated under the recipes. Under the products there is a description of the vitamins and minerals they contain.
“My Healthy Diet” →
Calorie Counter from FatSecret
In this application you can keep a food diary. Add the food you eat and the utility calculates calories and BJU. There are ready-to-eat meals and products from different brands. It is even possible to read the barcode of the product.
There is also an exercise diary in the app. You can find out how many calories you are spending on different types of physical activity.
By the way, the FatSecret service is also available on a PC, if it is more convenient for someone to count calories and activity there.
Application not found
YAZIO
In this application, you can select products from the database or scan a barcode, use recipes from the application or create your own.
There is also a burned calorie counter. And if you connect Google Fit, your workouts will be automatically downloaded to the app.
MyFitnessPal
In this calorie counter you can save your recipes, meals and even whole meals to save time.
There is also an activity counter with cardio and strength exercises. However, calories are not calculated in the latter. You can use this feature to quickly see what you did in the last workout. If you want to count the calories spent on weight training, add a new activity and add the calories manually.
The counter can be synchronized with fitness trackers or activity tracking applications MapMyFitness, MapMyRun, Garmin Connect and others.
How many calories you need to burn per day to lose weight | All about fitness and health
If you ask why exactly 700 calories, then this will be the answer to the question of how many calories a woman and man need to burn per day to lose weight. It is not clear where this figure came from? It’s very simple: according to research by scientists, if you burn 700 calories every day (if nothing else changes in your routine), then after six days or every six days, your body will lose 540 grams of weight.
There are many ways to burn calories, some of them are quick, but to burn that many a day, your fitness needs to be intense. Therefore, be sure to check with your doctor if there are any health restrictions before starting.
Don’t be afraid to split your workouts into several segments and have two workouts per day or more . In this case, the result is important. And it’s time for you to learn about exercise that burns calories.
There are many ways to burn calories and fat quickly, some of which I will mention below. But remember one thing: whenever you are physically active and moving, your body is wasting energy. Your task is to find those fitness activities that you like and start training.
Moreover, you now know how many calories you need to burn per day.
Running
If you are an experienced runner and skillfully use all types of running, then you are probably wondering how many calories running burns.If you run at a speed of 17.5 km / h for 30 minutes, then the calorie burn will be 707 units (with a weight of 75 km). But this is too intense a running pace. If you can’t support it, then don’t worry. You can run at half the speed – for an hour of jogging, you will burn the same amount of calories.
I want to mention that when running training for burning fat does not give the expected result, you need to change the approach to your training run – for example, an interval approach to running training is quite effective: alternating different running rates from jogging to sprint accelerations.
And remember, running workouts for fat burning work perfectly when you are comfortable with the exercise and do not have to literally “push” yourself into the workout.
Jumping rope
Knowing how many calories you need to burn per day, now let’s determine how many calories the rope burns. A person weighing 70 kg can burn a little over 750 units per hour of jumping rope. If you weigh more, then accordingly you will expend more energy and burn more fat. As we can see from the effectiveness of the jump rope for weight loss is no worse than running.
Jumping rope for an hour is pretty boring. In order to diversify it
, use some tricks: jumping on one leg then on the other, move forward, backward or to the sides. Engage under varying loads on your calves, thighs, buttocks, and abdominals.
Strength training
What happens if you add strength training to your cardio exercises to reduce weight? Will there be an effect? Will it help you burn calories and build muscle strength? On this we can safely say: yes.
Easily mix kettlebell and dumbbell exercises with cardiovascular fat loss workouts, or warm up with cardiovascular equipment such as a stepper. You can develop a workout plan in which you alternate equal portions of cardio and strength training, or practice a ladder approach that increases the difficulty or intensity of the workout. For example, you can start your workout with 10 repetitions of each of four exercises, two of which are cardio and two are strength, working on different muscle groups.
After completing the execution, repeat the same exercises but with nine repetitions each. Decrease the number of repetitions by one with each cycle during your workout. In the end, you will have to do each exercise one last time, and in total, you will do each exercise 55 times. Use a heart monitor, of which there are a lot of them now. Lifting weights is one of the easiest ways to increase the intensity of your weight loss workout and burn more calories.
Swimming
I included swimming here for a reason, you guessed it. And if you are wondering how many calories swimming burns, then I can say that you will burn 700 units in 68 minutes. In addition, swimming works out almost every muscle in your body, while gentle on your joints.
After we found out how many calories to burn per day, we also looked at some of the types of fitness that can effectively burn 700 calories. In fact, of course, there are many ways to burn such an amount of them, but this should not be your only and final goal when doing fitness.Choose the best time for training and exercise, thinking not only about moving calories out of your body, but that you are choosing a healthy lifestyle that will bring you, in addition to health, a great mood for the rest of the day.
Source: site “ All about fitness and health ”
How many calories you need to burn to lose weight
Updated: 23. 04.2021 11:35:07
04.2021 11:35:07
The amount of energy contained in foods and beverages is measured using calories.They are simply necessary for the normal functioning of the heart, blood vessels, respiratory and excretory organs, and the endocrine system. Our body actively consumes them even in complete rest. And when you create a calorie deficit, you can count on losing weight.
If you want to lose weight faster, many resort to careful calorie counting. The essence of this method is simple: the consumed energy should be more than the consumed one. However, you should learn to calculate the safe minimum of calories per day.An important rule: you must not allow a reduction in calories below 1200 kcal per day for women and 1600 kcal for men, because with such a deficit of energy, the body will begin to experience severe stress.
Optimal burning of calories per day to lose 2 kg
It is believed that to burn 1 kg of fat, you need to spend 7,700 kcal.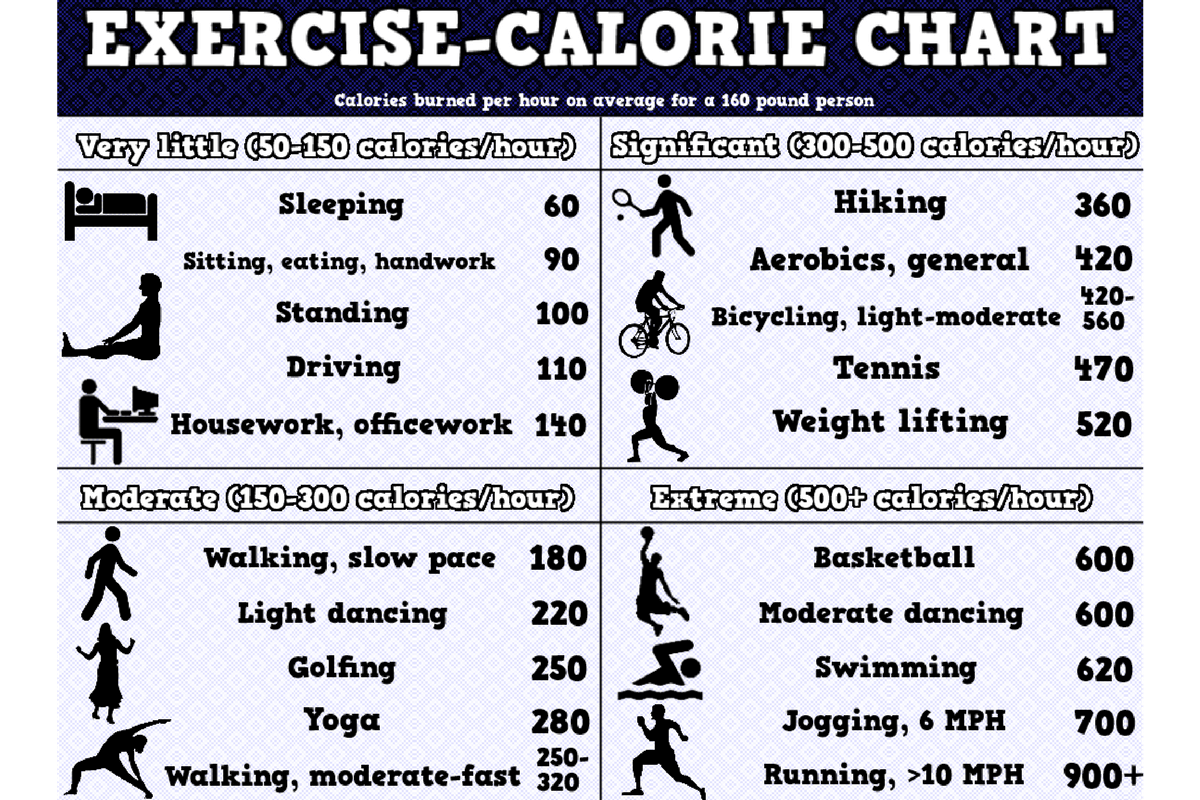 By dropping fat mass, it is optimal to lose weight by 2-4 kg per month. Losing weight without harm to health means dropping 0.5 kg of fat in 7 days.To do this, the calorie deficit should be 3850 kcal per week, and 550 kcal per day (3850: 7). This allows you to lose 2 kg of fat without harm to health in 4 weeks.
By dropping fat mass, it is optimal to lose weight by 2-4 kg per month. Losing weight without harm to health means dropping 0.5 kg of fat in 7 days.To do this, the calorie deficit should be 3850 kcal per week, and 550 kcal per day (3850: 7). This allows you to lose 2 kg of fat without harm to health in 4 weeks.
Calorie calculation using formulas
There is a widespread belief that women should consume about 2000 kcal per day, and men – at least 2500 kcal. But if a woman leads a sedentary lifestyle, then such a figure will be overestimated for her. Simple mathematical calculations will help you individually determine the right number of calories, allowing you to either maintain weight or lose it.
First of all, measure your height, weight and prepare a calculator. Next, use this formula:
women – 9.99 x body weight (kg) + 6.25 x height (cm) – 4.92 x age – 161;
men – 9.99 x body weight (kg) + 6.25 x height (cm) – 4.
 92 x age – 161 + 5.
92 x age – 161 + 5.
This formula will help you calculate how many calories will allow you to maintain the optimal weight and not gain excess.
And if you want to lose weight, then the calculations will have to be slightly modified taking into account your physical activity throughout the day. The results obtained according to the previous formula are corrected as follows:
multiplied by 1.2 with physical inactivity and complete absence of training;
multiply by 1.375 when doing fitness 1-2 times a week;
multiplied by 1.55 with regular training up to 5 times a week;
multiply by 1.725 at high physical exertion;
multiplied by 1.9 in professional sports.
Further, using an example, we will analyze how to calculate the number of kcal that allows you to maintain a stable weight and not gain weight. And also we will calculate the amount of kcal that must be burned daily in order to noticeably lose weight.
Visual Calorie Calculation
Take, for example, a young woman, 36 years old. With a height of 164 cm, she weighs 71 kg. Her excess weight is about 7-15 kg. This woman has low physical activity during the day.
We make calculations:
9.99 x 71 + 6.25 x 164 – 4.92 x 36 – 161 = 709.29 + 1025 – 177.12 – 161 = 1396.17 kcal;
1396.17 x 1.2 = 1675.4 kcal.
If she sticks to such a calorie content, she will feel comfortable and at the same time will not gain excess weight. But this woman wants to lose weight, so she needs to reduce calorie intake and increase physical activity.To start actively burning calories, it is recommended that she reduce their intake by 10-15%. In this case, a woman’s body should receive less by 168-250 kcal, that is, it should not go beyond 1425-1507 kcal.
After the next 5 kg weight loss, it is necessary to recalculate the calorie content, since with a decrease in weight, the body spends less calories on the general metabolism.
Ways to burn calories
In the body of healthy people, metabolism does not stop.You can burn calories not only during hours of sports. This process also continues during the digestion of food, during rest and sleep. It is quite enough for a week to carry out 3-5 workouts for 30-60 minutes. But at the same time, it is important to control your activity at other times during the day.
You can boost your metabolism in the following ways:
Exercise regularly every week. Choose the complexity of the exercises and their number for yourself so that your body gets used to regular sports.
Increase your mobility at home. You can burn calories during frequent walks in the fresh air, while moving around the house or walking up the stairs without using the elevator. Make practical use of the time while watching TV shows or shows – exercise on a stationary bike or do a simple set of exercises.
Change your eating habits.
 Eat more whole grains, fish, poultry, eggs, dairy products, vegetables and fruits.They force the body to burn more calories as they are absorbed. Cut back on processed foods and refined foods.
Eat more whole grains, fish, poultry, eggs, dairy products, vegetables and fruits.They force the body to burn more calories as they are absorbed. Cut back on processed foods and refined foods.If there is no time for training, then at least you should walk at least 10,000 steps a day. Well, if you start to systematically engage in fitness, then this will noticeably increase calorie consumption, speed up metabolism, strengthen the muscle corset, and also improve the proportions of the figure.
A little about the calorie content of products
Everything that you eat has its own nutritional energy value.It includes information about the amount of three main components – BJU (proteins, fats, carbohydrates). Each gram of carbohydrates contains 4 kcal, each gram of protein contains 4 kcal, and each gram of fat contains 9 kcal. High-protein diets tend to speed up your metabolism by 80-100 calories per day when compared to a low-protein diet.
You can burn calories faster by adding more protein to your diet.
You can lose weight faster if you exclude the following foods from your diet:
sugar, bakery products from first grade flour;
vegetables and fruits containing a lot of starch;
processed and artificially derived fats;
sweet compotes, store juices from packages;
alcohol.
However, keep in mind that the same amount of calories has completely different effects on hormones and metabolism. This is well illustrated by sucrose, which is composed of fructose and glucose. The latter is actively involved in the metabolism of any tissues of the human body, and fructose is metabolized only by the liver.
Fructose stimulates ghrelin (hunger hormone) and induces resistance to leptin (satiety hormone).If you consume a lot of fructose, then insulin resistance develops, the deposition of visceral fat increases, triglycerides accumulate in the cells of adipose tissue and the level of sugar in the blood rises. This is just one example to show that food choices should be made more thoughtfully.
This is just one example to show that food choices should be made more thoughtfully.
Losing weight and not harming your health is possible if you replenish your diet with such products:
various types of greenery;
vegetable salads;
unsweetened fruits.
To lose weight, establish a drinking regimen. Drink at least 1.5 liters of clean water a day. Consider not only the calorie content of foods, but also the amount of nutrients in them.
Popular Calorie Counting Apps
Special mobile applications help many people to calculate the calories eaten and burned. They all work in much the same way: you specify the amount of food eaten, as well as the types and amounts of exercise performed.
YAZIO
YAZIO Nutrition Diary contains information about a large number of products and ready meals. Their names can be entered by hand or their barcodes can be read using the built-in scanner. You can also use the catalog of 200 types of physical activity. The calories consumed and burned are combined into a single chart. 1 month history is saved.
You can also use the catalog of 200 types of physical activity. The calories consumed and burned are combined into a single chart. 1 month history is saved.
FatSecret
This Calorie Counter is very easy to use.This program is equipped with various modern tools to help you lose weight faster. With this application, you can keep a food diary, which allows you to monitor the food consumed. It has an exercise diary that allows you to record all the calories burned. And you can also use a dietary calendar that compares all the information collected.
Calorie
The advantage of Calorie is that this program works autonomously without being connected to the network.It can sync with Google Fit. All data about any physical activity added to that program is automatically loaded into Calorie. With this in mind, the daily calorie intake will be updated daily. Information about the food eaten is entered manually.
Calorie counting is an easy and convenient way to lose weight. You will gradually reduce the amount of energy consumed, using it wisely, and soon your body will acquire the desired shape.
You will gradually reduce the amount of energy consumed, using it wisely, and soon your body will acquire the desired shape.
Rate article | |
Total votes: 1, rating: 5 |
how and how much you need to run to lose weight
If you want to start running in order to lose weight, you must adhere to certain rules.
The body expends a lot of energy while running. At the same time, metabolism is normalized, calories are burned, metabolism is accelerated, and the work of the digestive system is improved.In addition, the muscles of the body are strengthened, the circulatory system is saturated with oxygen, the level of cholesterol in the blood decreases, and the work of the cardiovascular system improves.
Running is one of the simplest and most affordable methods of losing weight. At the same time, those who want to lose weight complain that they regularly run, but at the same time do not lose weight. The thing is that running for weight loss has many nuances that must be taken into account in order to get the desired effect.
The thing is that running for weight loss has many nuances that must be taken into account in order to get the desired effect.
So, let’s figure out how and how much to run to lose weight.
If you don’t want to read – listen to the podcast in iTunes and Yandex.Music
7 rules of running for weight loss
1. Run more than 40 minutes
For the first 40 minutes of running, the body runs on carbohydrates (glycogen is a complex carbohydrate stored in liver and muscle cells). And only then the transition to the stage of fat burning occurs. That is, to run to lose weight, you need at least 50 minutes at an average pace.
Perhaps this is the first thing you need to know on this topic.If you are a beginner, you will hardly be able to master 40 minutes at once. For beginners, we recommend alternating between slow running and brisk walking.
For a trained runner, the ideal method of losing weight would be a long cross-country race lasting at least an hour, with a monotonous speed, with a heart rate of no more than 150 beats / min, which corresponds to running with low intensity.
Training plans for marathon and half marathon. Download and start preparing today.
2. Eat right
You can often hear the phrase: “For you, runners, even if you eat a whole cake, everything will burn out during training.”Unfortunately, this is not so.
To reduce fat mass, you need to use more energy than you consumed. This means that any amount of physical activity works for the benefit of fat burning only when combined with proper nutrition.
3. Be sure to eat after training
Another misconception is that if you fast after exercise, you can burn more calories. If you want to use jogging to lose weight, don’t starve yourself.
The word “diet” does not always mean fasting, a sports diet is the right set of foods, their combination and quantity, as well as avoiding junk food: fast food, soda, chips, mayonnaise, flour, sugar, overcooked food, snacks on the go.
Include cereals, fresh vegetables and fruits in your diet. Drink plenty of clean water.
Drink plenty of clean water.
Read on: How many calories are burned while running
4. Train regularly
Light jogging once a week will be pleasant, but in terms of losing weight, it will be useless. To get rid of those extra pounds, run at least three times a week.
Winter, rain, wind – this is not a reason to cancel training. Now on the sports goods market there is a huge amount of equipment that allows you to train in any weather.
5. Alternate between different workouts
Long-term cross-country running, high-intensity interval training for the trained runner, cross-country running, strength training from the basic training complex – there are many ways to diversify your workout. For example, 10 jogging strength exercises with video.
6. Have fun training
Only by enjoying what you are doing, you can quickly achieve results. If every run for you is a psychological and physical torment, then the body will very soon begin to resist this stress, as a result, trauma, depression and invincible laziness are possible.
To cope with this usually helps your favorite music in headphones and bright fashionable outfit. Why aren’t you motivated?
7. Have patience
Having decided to start running in order to lose weight, you must clearly understand that without harm to health, the process of getting rid of extra pounds takes at least three months.
For everyone, this period is individual and depends on many factors: the amount of extra pounds, the metabolic rate, the number of workouts per week, the absorption of nutrients in the body, metabolic disorders, the desire or unwillingness to adhere to a diet.
And here are some recommendations on how to run correctly in order to lose weight and see the effect of training.
Read on: How to run properly: long-distance running technique
How to run to lose weight
The body burns glycogen for the first 40 minutes. Thus, the first 40-45 minutes of running will become a “warm-up” for those who want to lose weight, and fat will start to burn in the next 10-20 minutes. Run an hour at your own pace, not too fast or too slow.Jogging may work for you.
Run an hour at your own pace, not too fast or too slow.Jogging may work for you.
Don’t forget about recovery. Progress cannot be made without rest; muscles must regenerate. There should be at least one rest day per week. Don’t do more than two high-intensity workouts per week. Do at least 50% of your workouts for long crosses (at least 60 minutes).
Run over rough terrain for 50 to 90 minutes. This kind of running requires sufficient physical training. It combines a steady cross at a lower heart rate and interval stretches uphill with an increase in heart rate.Thus, a large number of calories are burned.
This technique will give a more tangible result, the weight dropped can be 30-40% more than when running in a stadium. But not suitable for beginners.
Watch your breathing, do not close your mouth while running, as you do while walking. Try to breathe through your mouth and nose at the same time, so you can capture more oxygen for each breath, supplying them with muscles that will work longer without acidification.
Watch your pulse.Aerobic exercise will be effective only if the heart rate is within the target zone. Subtract your age from 220 to calculate. The pulse during training should be no more than 80-90% of this value.
The pulse rate during a long run should never exceed 170 beats / min. If you see on your sports watch that your heart rate has already risen above 160, slow down.
Choose the right footwear. It is especially important for overweight runners to use shoes with extra cushioning.This is extremely important for the integrity of the joints. If you are obese, then don’t even try to run like professional athletes from the forefoot. Land on your midfoot and choose a park track and soft-surface stadium for training.
Contraindications to running for weight loss
Before you start running to lose weight, do not be lazy to visit a general practitioner to find out if you have any contraindications. Overweight people tend to have contraindications more often than others.
It is forbidden to run for people with heart disease, hypertension, bronchial asthma, peptic ulcer disease. It is necessary to temporarily stop training after abdominal surgical interventions. It is not recommended to run a lot for people with second or more degrees of varicose veins.
Read Next: How To Start Running: The Complete Beginner’s Guide to Running
90,000 How many calories per day do you need to lose weight?
There is no single norm for how many calories you need per day to lose weight.It is calculated individually for each person, taking into account his physical characteristics and lifestyle.
Where to start?
Before calculating how many calories there are to lose weight, you must first determine your daily intake. Essentially, calories are energy. Most of it is spent daily on maintaining the body’s work: breathing, heartbeat, digesting food, and so on. Scientists have found that:
- Men burn more calories than women.

- The older a person gets, the less energy he spends.
- During adolescence, pregnancy and illness, many more calories are needed.
- Physical activity increases the rate at which calories are consumed.
In addition, there are individual characteristics of the body, laid down by genetics, which determine the rate of calorie intake. However, on average, you can quite simply calculate how many calories to consume per day, so as not only not to get fat, but also to lose weight.
For example, you can use the formula of scientists Mifflin and San Geor. It was withdrawn in 2005 and has proven to be more effective than the Harris-Benedict variant. For the calculation you need:
- Weight multiply by 10.
- Increase height by 6.25.
- Age multiplied by 5.
Then all that remains is to add weight and height, and then subtract age. Then men add 5, and women subtract 161. The result is multiplied by the activity coefficient:
- 1.
 2 – lie on the couch for days or work in the office.
2 – lie on the couch for days or work in the office. - 1.375 – 3 times a week you remember that you need to go in for sports.
- 1.55 is an active athlete who works out 5 times a week.
- 1.725 – daily active training.
- 1.9 is a fanatical athlete, and during breaks you work as a loader.
That is, for a 35-year-old female accountant weighing 85 kg and 180 cm tall, the calculation will look like this (due to work, there is no time for sports):
((85×10) + (180×6.25) – (35×5) – 161) x 1.2 = 1966.8 calories.
This amount of energy will be enough for her to live and work calmly, while not getting fat. But in order to lose weight, you already have to calculate how many calories to consume.
How to lose weight by counting calories?
The golden rule of losing weight is spending more calories than you consume. But you can’t just take and drastically reduce the amount of food. The body does not like this. Instead, you need to take the calculator again and calculate how many calories you need to eat in order to lose weight.To do this, 15-20% must be subtracted from the previous result. That is, our woman accountant, in order to prepare for the summer, needs to absorb:
Instead, you need to take the calculator again and calculate how many calories you need to eat in order to lose weight.To do this, 15-20% must be subtracted from the previous result. That is, our woman accountant, in order to prepare for the summer, needs to absorb:
1966.8-20% = 1573.44 calories.
If she has an idea to get better, then everything must be done exactly the opposite. But it doesn’t end there. There are a few more conditions to consider:
- The number of calories consumed should not fall below 1200. Otherwise, the body will not have enough energy for life and the development of chronic diseases of various kinds is possible.
- You cannot calculate how many calories you need per day to lose weight, eat them in the morning and walk all day, starving. Be willing to break up meals 5-6 times. So the stomach and intestines will be constantly busy with work, the feeling of hunger will be less disturbing, and the diet as a whole will become much more pleasant.

- It is necessary to monitor not only calories, but also nutrients. Food should be varied so as not to provoke vitamin deficiency and other health problems.
- We must not forget about water.A large amount of fluid intake speeds up the metabolic processes in the body and removes toxins. This is a great help for fast weight loss.
Therefore, some nutritionists advise not to pay much attention to the amount of calories consumed. They believe that it is much more important to monitor the ratio of nutrients in the diet. And with the right balance, a person will quickly lose weight, regardless of the number of calories consumed.
By the way, there is another way to lose weight without cutting back on your diet.If you take our female accountant and give her a subscription to 5-round classes in a fitness club, it turns out that she will need not 1966.8 calories, but:
((85×10) + (180×6.25) – (35×5) -161) x 1.55 = 2540.45 calories.
That is, it turns out that she will even have to improve her diet a little and start eating more high-calorie foods, re-counting. And at the same time, she will still lose weight quickly enough.
And at the same time, she will still lose weight quickly enough.
Why is it impossible to greatly reduce the diet?
If you start counting how many calories you need to consume in order to lose weight, it may seem that the problem can be solved if you immediately reduce the amount of energy several times, or even to zero.But that’s not how the human body works. A fasting day once a week will create positive stress and can actually accelerate weight loss. With prolonged fasting, less positive changes are already taking place:
● hair falls out and skin condition worsens;
● arrhythmia develops;
● the person becomes irritable, easily depressed;
● the work of the digestive system and kidneys is disrupted;
● immunity weakens;
● concentration of attention and ability to think coherently decreases.
In this case, the body enters the “energy saving mode”. Metabolic processes slow down and weight loss occurs more slowly than it should. And after giving up fasting, there is a rapid weight gain.
And after giving up fasting, there is a rapid weight gain.
It is better to keep track of how many calories you need to eat in order to lose weight, and not rush anywhere. Healthy eating experts advise not to try to drastically lose 5-10-15 kg by cutting back on the calorie content of food. Natural weight changes should be about 1-1.5 kg per week.This is the most comfortable, on average, for a person, the rate of weight loss, to which one should strive.
How to lose weight on a treadmill
The treadmill is a great weight loss tool. When there is a simulator at home, it makes no sense to complain about the season, the weather and the lack of a park near the house.
Can you lose weight on a treadmill? The answer is yes, the main advantage of treadmills is the higher calorie consumption compared to other exercise machines.On average, for an hour of training, you can burn 700 Kcal.
Treadmills have heart rate sensors and a built-in display that displays workout metrics – calories burned, distance, speed, workout time. Built-in programs (depending on treadmill model) add variety to your workouts. Slimming treadmills contain special programs aimed at burning fat, interval training for weight loss.
Built-in programs (depending on treadmill model) add variety to your workouts. Slimming treadmills contain special programs aimed at burning fat, interval training for weight loss.
Rules for effective training on a treadmill
To lose weight on a treadmill, you must follow a number of rules.Before you start training, you should choose comfortable, light clothing, wear sneakers for running. During the workout, it is recommended to drink still water in small sips. You need to take food 1 hour before and 1 – 1.5 hours after class.
1. Start with warm-up
Start with a slow walk of 3-4 km / h, gradually increasing the speed. This will avoid premature fatigue and injury.
2. Monitor your heart rate
By increasing the heart rate, calories are burned.Before exercising on a treadmill, you need to calculate the maximum heart rate (MPR), which depends on age. Calculation formula: “MPP = 220 – age in years.” If you are 35 years old, then the MPP = 185 beats / min.
It is recommended to carry out most of the training at a heart rate equal to 70 – 75% of the MPE and not go beyond 80% of the MPE, this is fraught with overloading the cardiovascular system.
Some treadmills are equipped with functions that, after age is entered, track the pulse and change the intensity of the workout for maximum results, preventing overshooting and overloading the heart.
3. Change the training speed
It is recommended to change the training speed or the angle of inclination of the walking belt every 5-15 minutes, i.e. make it interval. This approach will prevent premature fatigue from monotonous exercise. In addition, changing your heart rate speeds up your metabolism, which will help you lose weight faster.
4. End of workout
It is important to finish your workout correctly.Slowly reduce your speed from running to walking. Do not stop exercising at peak intensity after the time has elapsed – this is harmful to the muscles, heart and engine of the treadmill.
5. How long should you run on a treadmill to lose weight?
For weight loss, regular exercise is important. The optimal option is 3-5 times a week. In the first month, 2-3 times may be enough. The duration of the lesson is at least 30 minutes.
6.Don’t overdo it
It is worth soberly assessing your strengths and starting small. For a beginner, 2 minutes may be enough to exceed 80% of the MUF. The “week of torment and muscles will get used” approach is wrong, you cannot give extreme loads to an unprepared body. It may be worth learning how to walk quickly first.
Never start a treadmill exercise if you have headaches, fever, or an injury that has not completely healed.
Training programs: weight loss with treadmill
For beginners
- Walking for 5 minutes, speed 6-7 km / h.
- Alternation: 3-5 minutes jogging / walking 5 minutes.
- End – walk 5 minutes.
Walking at a speed of 6-7 km / h, the heart rate should be 55-75% of the MPH. The running time is chosen according to your well-being.
The running time is chosen according to your well-being.
Slimming workout
- Jogging for 5 minutes, speed 8-9 km / h (after warm-up).
- Alternating walking / jogging, gradually decreasing the walking time.Walking for 2-3 minutes, running for 5-10 minutes.
- Jogging for 5-7 minutes, speed 7-8 km / h.
Interval Slimming Workout
For people with good physical fitness. It will help you lose weight quickly by running on a treadmill. To begin with, you can do this:
- Run for 5 minutes, average speed.
- Intensive running for 2 – 3 minutes, high speed.
- Medium intensity running – 5 minutes.
- Alternating Running – Medium / High speed, gradually decreasing the high speed running time as needed.
- End – run for 5 minutes, medium speed.
You can lose weight on the treadmill, but it will help you not only with this – after a few weeks your general well-being will improve. When exercising on a treadmill, blood pressure returns to normal, breathing will become easier, and sleep will improve.Over time, having achieved your goal of losing weight on a treadmill, you can simply maintain the tone of the body.
When exercising on a treadmill, blood pressure returns to normal, breathing will become easier, and sleep will improve.Over time, having achieved your goal of losing weight on a treadmill, you can simply maintain the tone of the body.
You can buy a treadmill in our online store.
90,000 how many calories are burned in an hour and 30 minutes – blog Mir-Sporta.com
Exercise bike and calories – one of the most popular topics for discussion on the Internet. The controversial nature of this issue is breaking records. People are interested not only in how many calories on an exercise bike can be burned in one workout without prejudice to their health, but also the specific place of this sports unit on the pedestal, where they stand next to:
- Treadmill;
- Elliptical Trainer.
Which is more efficient? What’s better? Which is safer? Which is more suitable for men and which is more suitable for women? We want to talk about all this and many other things in our new article. And let’s start with the benefits.
And let’s start with the benefits.
Advantage of the exercise bike over other cardiovascular equipment
Let’s put safety first. Which simulator of all existing in nature will be the safest? Let’s not rush to conclusions and say that the safest ride on a stationary bike, along the way, destroys calories, but let’s start thinking logically.
The treadmill, for all its effectiveness, is by no means the safest cardiovascular equipment. Despite the fact that its height does not exceed 5-10 centimeters from the floor, it is still a nonzero parameter. And from this height you can fall. And if you take into account that this is the height “moving” under your feet, then an hour on a stationary bike in a sitting position looks much safer.
An exercise bike that burns calories is the best option not only for those people who have changed their seventh decade, have information in their medical records about impaired coordination of movements, and suffer from sudden dizziness.
Suppose that you have not been involved in sports for N number of years. But you want to start a regular cardio exercise that can get rid of both excess weight and arrhythmias. Is the treadmill “asking for”? But no.
Even if you are full of energy 30-year-old person , do not forget that as a result of hyperventilation of the lungs , which is carried out during any cardio load, you may feel dizzy and coordination of movements may be disturbed .This can happen in as little as half an hour on the treadmill or ellipsoid (which many call the orbit track).
This will easily happen in 30 minutes on the exercise bike . But on it you are in the maximum stable position . You can stop training by stopping pedaling. On ellipsoid , by the way, also you can stop almost immediately . But on the treadmill , you still need to remember about the emergency button (“emergency”) stop , which is not so easy to do in case of a sudden clouding of consciousness.
But on the treadmill , you still need to remember about the emergency button (“emergency”) stop , which is not so easy to do in case of a sudden clouding of consciousness.
Exercise bike Oxygen Satori UB HRC
Brand: Oxygen Fitness
Loading system: electromagnetic
Number of load levels: 16
Flywheel weight: 10 kg
Maximum user weight: 150 kg
Number of programs: 21
39 990 ₽
from 1 111 ₽ / month
Add to compare
Add to favorites
If you are attentive and observe safety precautions, you may have noticed that often a wire runs to this “alarm” button, and the clip with which it ends is attached to the student’s clothes.
But how often do those who run on the track wear it? Very infrequent. And a sharp deterioration in well-being occurs, on the contrary, quite often. And, what a shame, suddenly.
The advantages of a stationary bike over an ellipsoid are obvious to everyone who has practiced both on an ellipsoid and an exercise bike at least once. Conclusions can be drawn by practicing for about an hour. An exercise bike burns fat better. What result in calories did you manage to “get” from the orbit track?
Conclusions can be drawn by practicing for about an hour. An exercise bike burns fat better. What result in calories did you manage to “get” from the orbit track?
The author of this text, engaged in sports at a semi-professional level about 12 years , burns on an ellipsoid 220-230 Kcal for 1 hour .And riding on an exercise bike “destroys” calories not exactly the same as on a treadmill, where both the upper and lower muscle groups are involved, but quite decently – is about 500 kcal , if you “do not strain too hard”.
To the question of how much an exercise bike burns and under what conditions, we will return a little later, but to summarize the chapter about its advantages, we can conclude that it is an exercise bike purchased on Mir-Sporta.com, how many calories it would not burn, is the golden mean between the treadmill and the ellipsoid.The orbitrek certainly has its advantages (we will not go into the particularities of pumping individual muscle groups, which can be worked out especially well on the ellipsoid). We are more interested in what pumps and how much the exercise bike burns.
We are more interested in what pumps and how much the exercise bike burns.
Is an exercise bike effective for burning calories?
Believe it! If an exercise bike that burns calories could talk, it would ask exactly the same question to someone who is going to start training on it.
But here’s the thing: an exercise bike burns your calories in direct proportion:
- The degree of your efforts that you make during classes on it;
- Intensity of the lesson;
- The speed of metabolic processes that are invisibly carried out in your body, which does not depend on you;
- A diet that you can, depending on your desire and capabilities, both follow and not follow (yes, a hearty breakfast or lunch that you ate before starting classes also determines how much kcal is burned on an exercise bike).
The one who slowly pedals in the most “light” training mode, looking at the watch or out the window, and enjoying life, is unlikely to burn more than 250 kcal per hour on the coolest exercise bike.
Well, a person who, with all his urine, turns an old “ belt ” or “ shoe ” exercise bike, can lose and 850 kcal .
Spin bike Diadora Racer 23
Brand: Diadora
Loading system: shoe
Flywheel weight: 23 kg
Maximum user weight: 140 kg
Net weight: 50 kg
Warranty: 1 year
46 400 ₽
30 000 ₽
from 833 ₽ / month
To compare
To favorites
And it is not at all a fact that he will be right, because the level of permissible load is a completely separate topic that should be discussed not so much on the Internet as with a personal therapist or specialized medical specialist dealing with the treatment of existing chronic diseases. So!
How many calories are burned per hour?
If we put this indicator at the forefront, focusing on how an exercise bike destroys calories per hour, it turns out that we take into account the average pace for a person who is able to withstand such a training over time. But it is very important and must always be kept in mind that a calorie is just a conventional unit of measurement of energy, which does not mean the number of lost grams or, moreover, kilograms. She tells us only about a certain release of heat from our body. But only.
But it is very important and must always be kept in mind that a calorie is just a conventional unit of measurement of energy, which does not mean the number of lost grams or, moreover, kilograms. She tells us only about a certain release of heat from our body. But only.
Real weight loss depends on your model of behavior, the natural outflow of energy during the day (if you are a courier who spends life on the move, then you hardly need an exercise bike and counting calories!)
And if you worked out effectively for an hour on a stationary bike, and then occupied McDonald’s with friends for two hours to enjoy high-calorie big macs and a couple of kilograms of fried potatoes, then is it any wonder if, in the evening, standing on the scale, you see a significant increase in weight?
30 minutes on a stationary bike or 3 hours? What difference does it make how much you worked out if you left the gym for a barbecue, where you can more than make up for the lost?
Very important and extremely interesting! How much does an exercise bike burn in the case of a thin person, and in the case of someone who has more weight?
It turns out that the numbers will be completely different.Because overweight people lose significantly more calories. This is what is meant when we read judgments on the forums that “fat flies off very quickly.”
Let’s take a fairly modest speed – 14-16 km / h , which corresponds to the “light” mode of movement. For people , who weighs only 50 kg , the exercise bike will destroy only 270-272 calories per hour , and for the one who weighs 65 kilograms – 350 .But these are the minimum speeds, and what is the picture of those who train at the limit?
Let’s set the “high-speed echelon” 35-37 km / h , on which a trained and well-trained athlete can hold out. For a 50-kilogram athlete, an exercise bike burns approximately 770-780 calories , and for an athlete who weighs 65 kilograms , as much as is 200 kcal more than .
How much is burned in 30 minutes?
Not every person has the strength and endurance to pedal an exercise bike for an hour.And not every person in the realities of the world around us will allocate 60 minutes for training. Much easier to do 30.
The question – how many calories on an exercise bike can be destroyed in half an hour, does not imply that you need to divide the hourly indicators in half. Most modern sports equipment can allow you to complete the program “with a bang” in 30 or even 20 minutes.
Is it realistic to increase efficiency, to make the exercise bike burn calories more intensively, but in the “maximally compressed” period of time? Yes.
If you want to buy an exercise bike, first look into any gym. You will see that on almost all modern units the minimum training time is 20 minutes . It can be made smaller. Or, on the contrary, you can put on an hour and a half. But the manufacturer, as it were, points out to us that an exercise bike (of different, we repeat, brands and brands) burns calories very productively in half an hour and in a third.
Please note: the next thing that prompts you to select the on-board computer is the program.And she, again, is different. 20 minutes is not always “light duty” on the flat road .
Where is more effective than Hills or Interval training . It simulates movement in different planes. At first, you seem to be driving in a straight line, and then the load suddenly increases, and you … sweat, because it seems to you that you are going uphill. At maximum amplitudes, you get the impression that you are driving almost … vertically.Needless to say, such a workout will squeeze all the juice out of you?
By the way, subconsciously we always avoid these “Hills” and programs, after which the tongue falls on the shoulder. Therefore, the claim that software can replace the services of a coach is very controversial. It depends on whom! For a disciplined person who decides to do away with extra calories and pounds, yes. And for those who periodically “sit down” on a bicycle for 10 minutes to hold a meeting by phone or a detached dialogue, alas, no!
A couple of tips to speed up your calorie burning
- When buying an exercise bike, remember: How many calories “disappear” depends not only on the amount of effort you put on the sports machine, but also on what strategy you follow.
- Keep in mind the simple fact that you will achieve maximum efficiency by alternating hard training with light . Long with short. This is very important, because a huge number of people “got out of the race” during the first month (yes, there! – weeks), because they started training too hard.
- Three hard workouts in a row , carried out without the allotted day for the recovery of the body, and your body, your cardiovascular system begin to “accumulate” harm. The heart wears out faster than instead of getting stronger and building up its potential.
- A light workout after yesterday’s hard , when you are already barely pedaling after you gave your best at 35 km / h yesterday, overcoming “hills” – this is a very smart decision . You support the body, take care of it, do not overload not only the cardiovascular system, but also the nervous one. will not be overwhelmed by fatigue and depression .
- Interleaving the load mode is also very useful during the actual session . Let’s say you pedal the simulator in light mode for more than 5 minutes. This is a great excuse to “tense up” and scroll the next minute to 30-35 km / h. Hard? But it is this “jerk”, alternated with a lighter version of training, which makes it possible for the body not to “adapt” to the same type of load. After all, a workout that takes place in the same format, not only does it start to get boring, as a result of which the simulator then gathers dust in the corner for years, it also becomes ineffective.

 At the beginning of a meal, take slightly less than what you think you’ll eat. If you’re still hungry, eat more vegetables or fruit.
At the beginning of a meal, take slightly less than what you think you’ll eat. If you’re still hungry, eat more vegetables or fruit. gov/ten-tips-enjoy-your-food. Accessed Dec. 4, 2020.
gov/ten-tips-enjoy-your-food. Accessed Dec. 4, 2020.

 Studies show that the combination of diet and exercise are compounded to increase weight loss more than the equivalent of one method alone. One theory is that the exercise increases metabolism which rev’s the fat burning even more. Example: If you cut 200 calories a day from your diet and burned 300 calories a day by exercising, you’d lose about one pound per week. Compare that to the other examples above—so you’re losing weight at about the same rate without making such extreme changes to your diet or exercise routine.
Studies show that the combination of diet and exercise are compounded to increase weight loss more than the equivalent of one method alone. One theory is that the exercise increases metabolism which rev’s the fat burning even more. Example: If you cut 200 calories a day from your diet and burned 300 calories a day by exercising, you’d lose about one pound per week. Compare that to the other examples above—so you’re losing weight at about the same rate without making such extreme changes to your diet or exercise routine.
 92 x age – 161 + 5.
92 x age – 161 + 5. Eat more whole grains, fish, poultry, eggs, dairy products, vegetables and fruits.They force the body to burn more calories as they are absorbed. Cut back on processed foods and refined foods.
Eat more whole grains, fish, poultry, eggs, dairy products, vegetables and fruits.They force the body to burn more calories as they are absorbed. Cut back on processed foods and refined foods.
 2 – lie on the couch for days or work in the office.
2 – lie on the couch for days or work in the office.