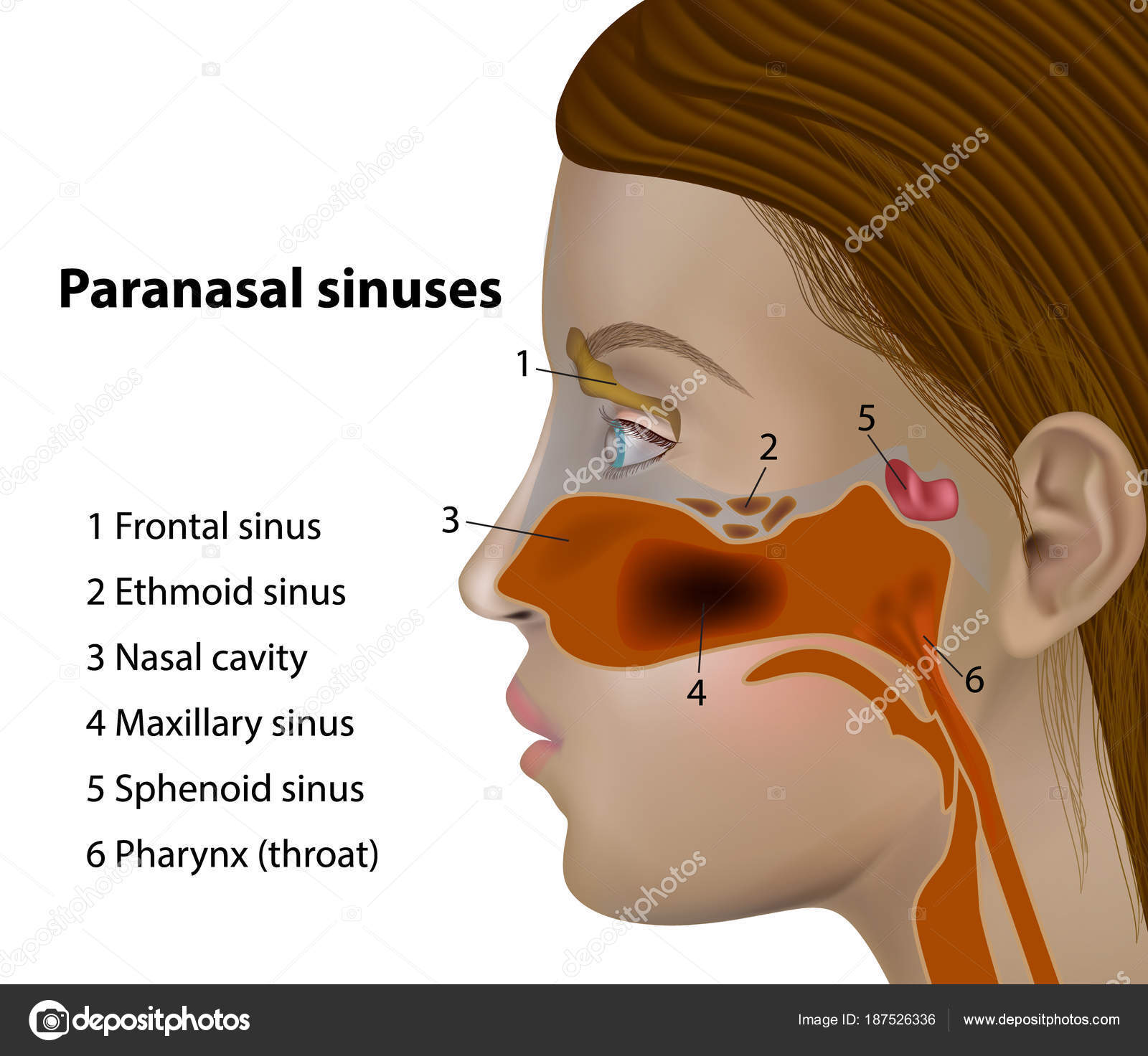
Sinus one side. Sinus Infection on One Side: 5 Key Signs and Symptoms to Watch For
What are the telltale signs of a sinus infection affecting only one side. How can you distinguish between sinusitis and rhinitis. When should you seek medical attention for sinus symptoms.
Understanding Sinusitis: More Than Just a Common Cold
Sinusitis, often confused with rhinitis, is a condition that affects millions of people worldwide. While both conditions can cause similar symptoms, understanding the key differences is crucial for proper diagnosis and treatment.
Rhinitis refers to inflammation of the nasal passages, typically caused by a virus (common cold) or allergens (hay fever). In contrast, sinusitis involves inflammation of the sinus cavities located behind the cheeks and forehead. These cavities drain into the nose through small passages, which is why both conditions can lead to nasal discharge.
Adding to the complexity, sinusitis frequently develops following a bout of rhinitis. While viruses and allergens can trigger both conditions, sinusitis may also result from bacterial or fungal infections.

The Importance of Accurate Diagnosis: Sinusitis vs. Rhinitis
Distinguishing between sinusitis and rhinitis is crucial for effective treatment. Antibiotics, rarely beneficial for rhinitis, are often necessary for sinusitis. This distinction becomes even more critical when symptoms are localized to one side of the face.
Can sinusitis affect only one side? Yes, it’s quite common for sinusitis to manifest unilaterally, affecting the sinuses on just one side of the face. This one-sided presentation can be a key indicator in differentiating sinusitis from other conditions.
5 Tell-Tale Signs of a Sinus Infection
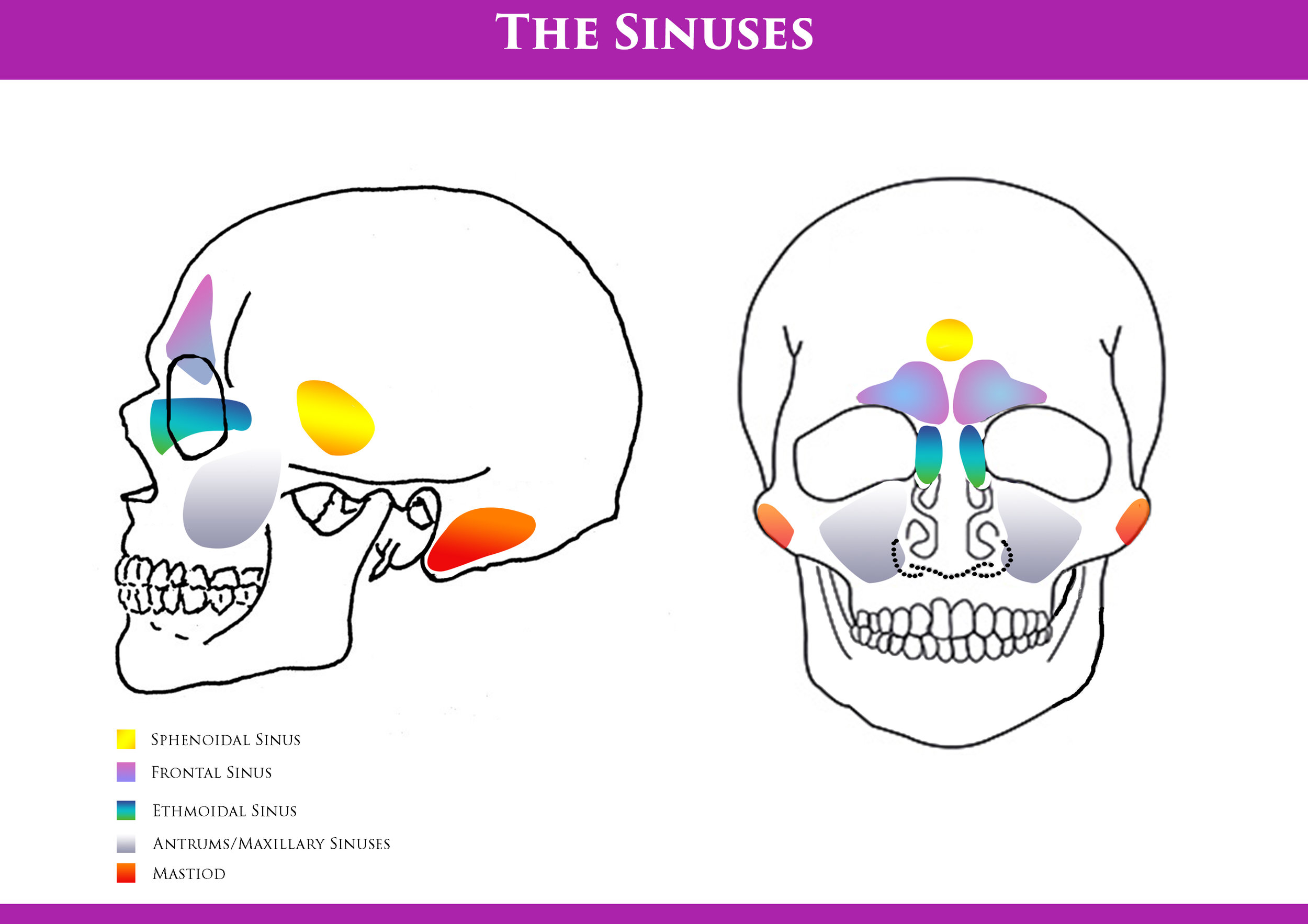
1. Localized Headaches and Facial Pain
One of the most significant indicators of sinusitis is pain, which is less common in rhinitis. The location of this pain can provide valuable clues about which sinuses are affected:
- Frontal sinuses: Pain behind the forehead
- Maxillary sinuses: Discomfort behind the cheeks
- Ethmoid sinuses: Pain behind the nose
- Sphenoid sinuses: Ache near the eyes
Is the pain more intense on one side? Unilateral or highly localized pain is strongly suggestive of a sinus infection rather than generalized head pain. Sinus headaches often worsen upon waking due to fluid accumulation overnight and can be exacerbated by changes in air pressure.
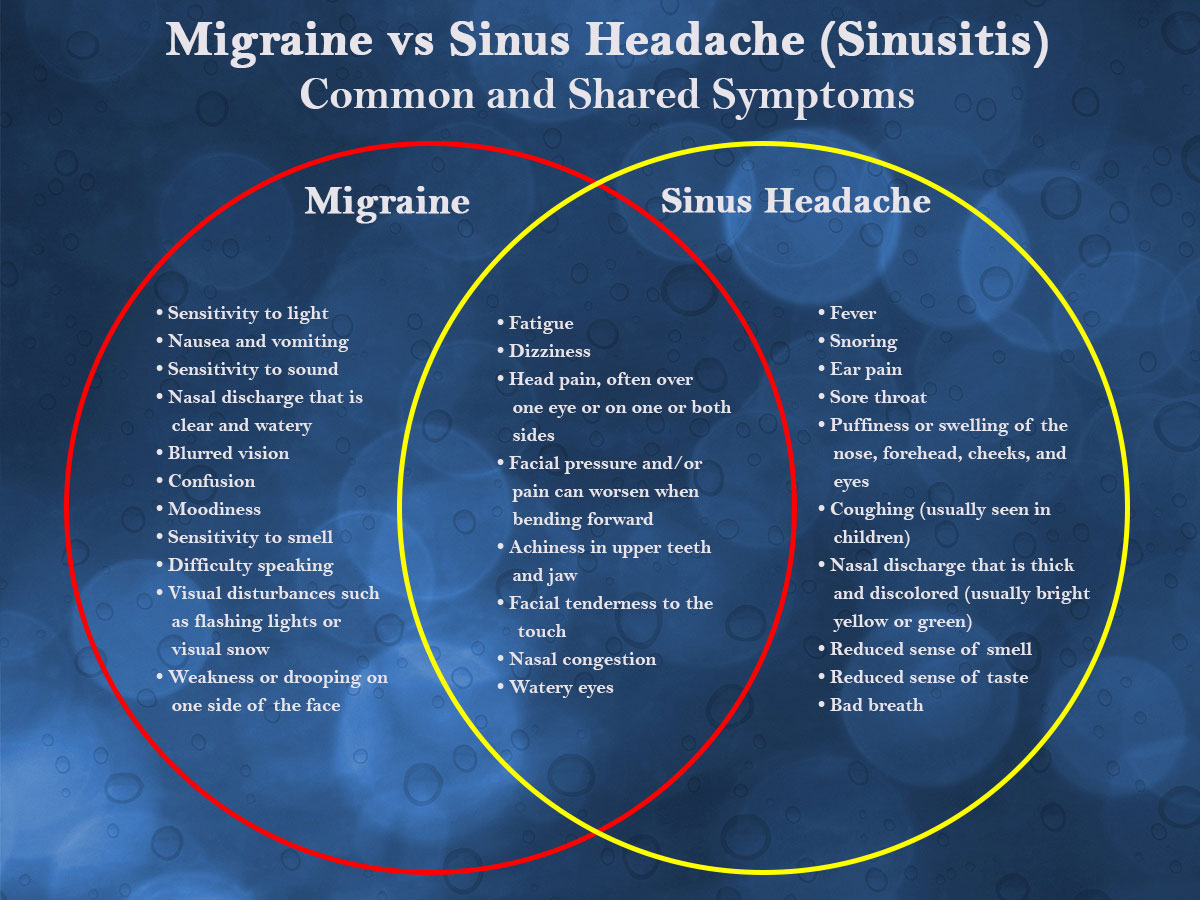
2. Distinctive Nasal Discharge
The characteristics of nasal discharge can help differentiate between rhinitis and sinusitis:
- Rhinitis: Typically produces thinner, clear or slightly yellow discharge from both nostrils equally
- Sinusitis: Results in thicker, darker green or brown discharge, sometimes with blood
Is the discharge more prominent from one nostril? Dark or bloody secretions from only one side strongly indicate a sinus infection rather than a common cold.
3. Fever
Unlike the common cold, sinusitis can often cause an elevated body temperature exceeding 100.4째F (38째C), which is considered a fever. Over-the-counter medications like ibuprofen or acetaminophen can help manage fever and discomfort, but it’s always wise to consult a healthcare provider before starting any new medication regimen.
When should you seek immediate medical attention for fever? For infants under three months with signs of sinusitis or fever, prompt medical evaluation is crucial.
4. Localized Symptoms
While the common cold tends to produce symptoms in multiple areas (nose, throat, bronchi, lungs), sinus infections are usually more localized to the affected sinus. Symptoms like phlegm production from the lungs, voice changes, intestinal issues, chest pain, or breathing difficulties suggest conditions other than sinusitis.

What symptoms warrant immediate medical attention? Chest pain, breathing difficulties, or bloody phlegm from coughing should prompt an immediate doctor’s visit.
5. Persistent Symptoms
Duration of symptoms can be a key differentiator between a common cold and sinusitis. Cold symptoms typically resolve within 10-14 days, while sinusitis often follows a cold and can persist much longer.
- Acute sinusitis: Can last up to four weeks
- Chronic sinusitis: May persist for months
How long should you wait before seeking medical advice? Any cold-like symptoms lasting beyond two weeks warrant evaluation for possible sinusitis.
Unilateral Sinusitis: When One Side is Affected
Sinusitis affecting only one side of the face, or unilateral sinusitis, is not uncommon. This condition can occur when only one sinus or a group of sinuses on one side becomes infected or inflamed. The unique presentation of unilateral sinusitis can sometimes lead to misdiagnosis or confusion with other conditions.
Symptoms Specific to One-Sided Sinus Infections
When sinusitis affects only one side, you may experience:
:max_bytes(150000):strip_icc()/sinus-infection-vs-covid-19-5197067-FINAL-d09ade4deec242229c3a51db8e3238d1.jpg)
- Pain or pressure localized to one side of the face
- Swelling around one eye
- Nasal congestion primarily in one nostril
- Discolored nasal discharge from one side
- Toothache on the affected side (particularly with maxillary sinusitis)
Why does sinusitis sometimes affect only one side? This can occur due to anatomical variations, such as a deviated septum, or localized trauma or irritation to one sinus cavity.
Diagnosing Sinusitis: When to See a Doctor
While many cases of sinusitis resolve on their own or with over-the-counter treatments, certain situations warrant professional medical attention. Consult a healthcare provider if you experience:
- Symptoms persisting beyond 10 days
- Severe symptoms, particularly if one-sided
- High fever (above 101.5째F or 38.6째C)
- Worsening symptoms after initial improvement
- Changes in vision or severe swelling around the eyes
How do doctors diagnose sinusitis? Diagnosis typically involves a physical examination, review of symptoms, and sometimes imaging studies like CT scans or nasal endoscopy.
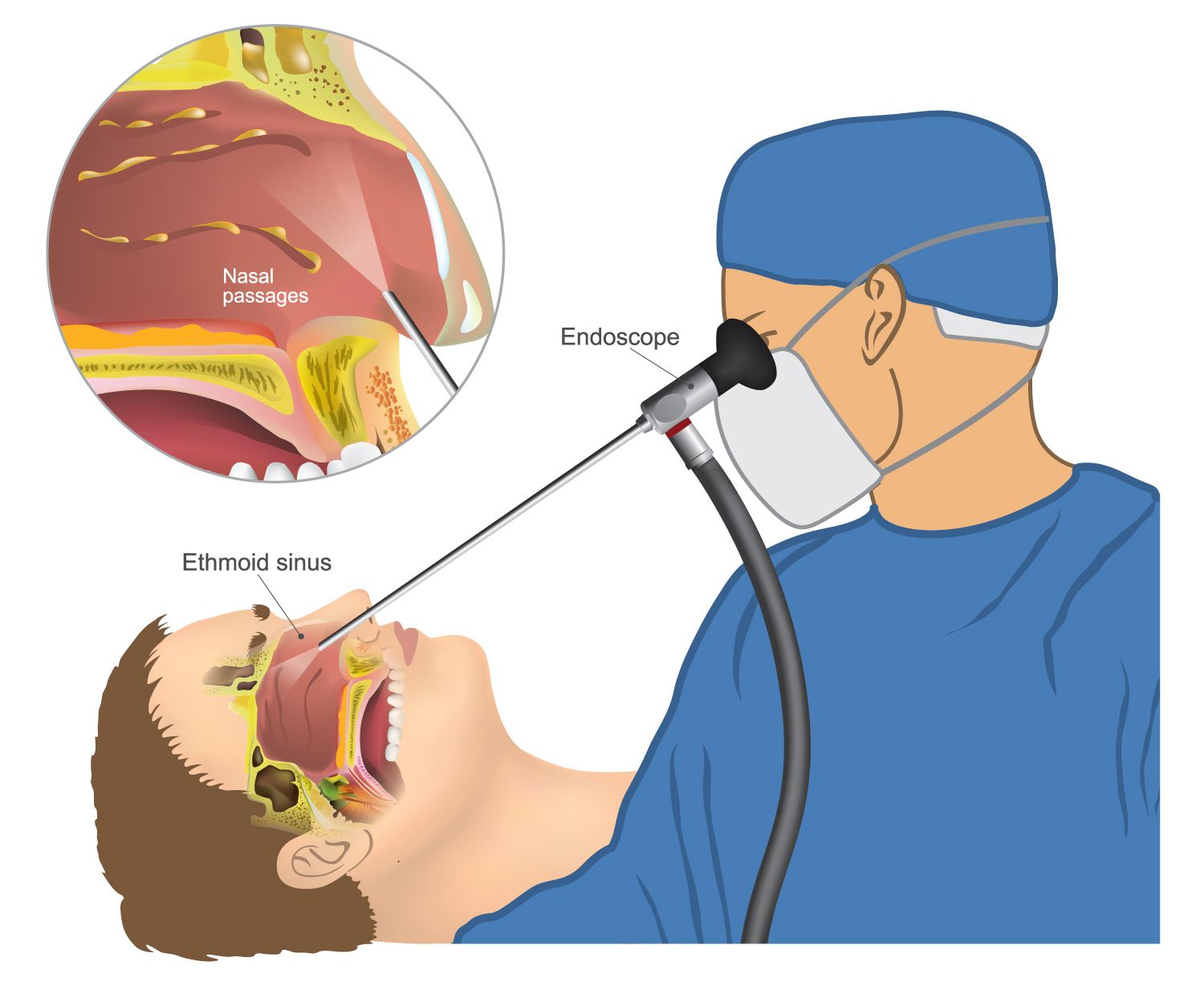
Treatment Options for Sinus Infections
The approach to treating sinusitis depends on its cause, severity, and duration. Treatment options may include:
- Nasal irrigation with saline solution
- Over-the-counter pain relievers and decongestants
- Nasal corticosteroid sprays
- Antibiotics (for bacterial infections)
- Antihistamines (if allergies are a contributing factor)
In cases of chronic or recurrent sinusitis, especially when symptoms are predominantly one-sided, more aggressive treatments may be necessary. These could include:
- Oral corticosteroids
- Immunotherapy for underlying allergies
- Endoscopic sinus surgery
When is surgery considered for sinusitis? Surgery is typically reserved for cases that don’t respond to medical treatment or for structural issues contributing to recurrent infections.
Preventing Sinus Infections: Proactive Measures
While not all sinus infections can be prevented, several strategies can reduce your risk:
- Practice good hand hygiene to avoid viral infections
- Use a humidifier to keep nasal passages moist
- Avoid known allergens and irritants
- Stay hydrated to thin mucus secretions
- Avoid smoking and secondhand smoke
- Manage allergies effectively
For those prone to recurrent sinusitis, especially unilateral cases, additional preventive measures may include:
- Regular nasal irrigation with saline solution
- Use of nasal corticosteroid sprays as directed by a healthcare provider
- Addressing structural issues like a deviated septum
Can dietary changes help prevent sinusitis? While not a cure-all, some individuals find that reducing dairy intake or increasing consumption of anti-inflammatory foods can help manage sinus symptoms.
The Impact of Sinusitis on Quality of Life
Chronic or recurrent sinusitis, particularly when it affects one side predominantly, can significantly impact an individual’s quality of life. Common effects include:
- Chronic fatigue due to poor sleep quality
- Reduced productivity at work or school
- Social isolation due to persistent symptoms
- Anxiety or depression related to chronic pain and discomfort
How can you manage the psychological impact of chronic sinusitis? Strategies may include stress management techniques, joining support groups, and working with mental health professionals experienced in chronic illness management.
Emerging Research and Future Treatments
The field of sinus health is continuously evolving, with new research shedding light on the complexities of sinusitis and potential treatment innovations. Some areas of ongoing research include:
- The role of the microbiome in sinus health and disease
- Novel drug delivery systems for more effective topical treatments
- Immunomodulatory therapies for chronic sinusitis
- Minimally invasive surgical techniques for refractory cases
What promising treatments are on the horizon for sinusitis? Researchers are exploring treatments like phage therapy for antibiotic-resistant infections and personalized medicine approaches based on individual patient factors.
Understanding the nuances of sinusitis, particularly when it affects one side predominantly, is crucial for effective management and treatment. By recognizing the signs, seeking timely medical attention, and following appropriate treatment plans, individuals can significantly improve their quality of life and reduce the impact of this common yet often misunderstood condition. As research continues to advance our understanding of sinus health, we can look forward to more targeted and effective treatments in the future, offering hope to those who struggle with chronic or recurrent sinusitis.

Five Signs You Might have a Sinus Infection
12|07|2018
Sinusitis is an often-misused term. It is frequently, but incorrectly, used to refer to a similar, but distinct condition called rhinitis. Rhinitis is inflammation of the nasal passages (not the sinuses), usually by a virus (the “common cold”) or an allergen (“hay fever”). Sinusitis, on the other hand, is inflammation of the sinus cavities, which are behind the cheeks and forehead, not in the nose at all. But, each of the sinuses drains through tiny “passages” into the nose. Therefore, both conditions cause nasal discharge, leading to the confusion between them. To add to the confusion, sinusitis often follows rhinitis. Similar to rhinitis, sinusitis may also be cause by a virus or allergen but additionally, can be caused by bacteria or fungi.
Since antibiotics are almost never helpful with the much more common rhinitis, but are often indicated for sinusitis, it is important to distinguish the two conditions. So, how does one know the difference? Below are five signs of a sinus infection or sinusitis:
So, how does one know the difference? Below are five signs of a sinus infection or sinusitis:
Headaches
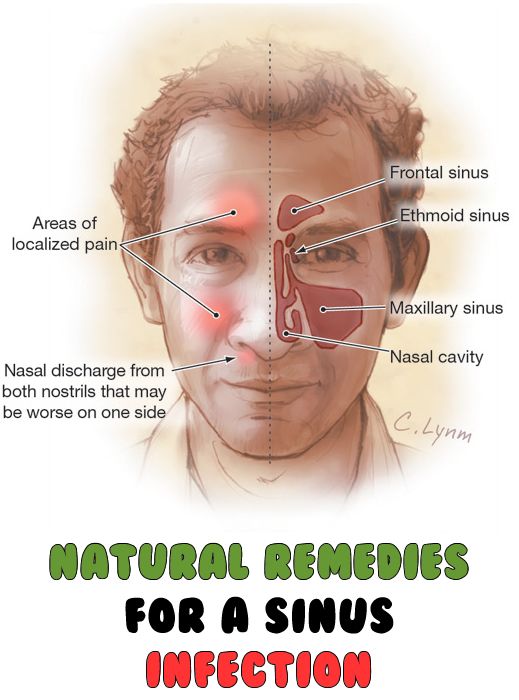
Pain is among the most significant signs of sinusitis and is not common with rhinitis. There are sinuses located behind the forehead (frontal sinuses), behind the cheeks (maxillary sinuses), behind the nose (ethmoid sinuses), and near the eyes (sphenoid sinuses). When any of these develops an infection, the resulting swelling and inflammation usually produces pain similar to a headache.
Pain may be felt generally throughout the head but will more often be experienced in the specific part of the head with the infected sinus. Therefore, one sided, or very localized pain is more suggestive of a sinus infection that global head pain. Sinus headaches are often worse upon awakening in the morning due to the fluids that accumulated throughout the night. Changes in air pressure can also worsen sinus headaches.
The nasal drainage of rhinitis is usually thinner, clear or slightly yellow in color and expressed from both nostrils equally.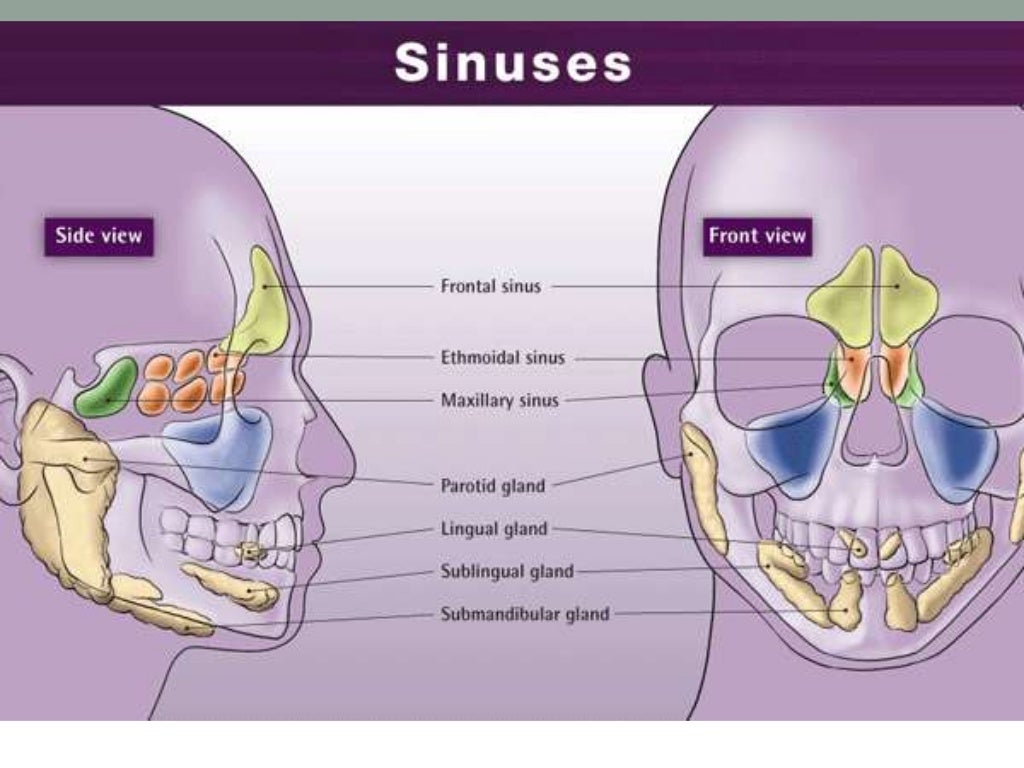 In contrast, the nasal drainage associated with a sinus infection is thicker, darker green or brown, and sometimes bloody. Importantly, since sinus infections are most often one-sided, dark or bloody secretions from only one nostril strongly suggest a sinus infection rather than a cold.
In contrast, the nasal drainage associated with a sinus infection is thicker, darker green or brown, and sometimes bloody. Importantly, since sinus infections are most often one-sided, dark or bloody secretions from only one nostril strongly suggest a sinus infection rather than a cold.
Fever
More often than the common cold, sinusitis can cause an increase in your body temperature over 100.4 degrees Fahrenheit, the point at which temperature elevation is considered to represent a fever. You can relieve the fever and some of the discomfort by using over-the-counter medication such as Ibuprofen (Advil) and acetaminophen (Tylenol). As with all over-the-counter medications, you should consult your doctor prior to taking them. Children under three months of age who exhibit signs of sinusitis or fever should see a doctor right away.
Unlike the common cold, that tends to produce symptoms in multiple locations including the nose, the throat, the bronchi and the lungs, sinus infections are much more specific to the sinus that is infected. Therefore, phlegm production from the lungs, loss of voice, intestinal symptoms, chest pain or trouble breathing all suggest conditions other than a sinus infection. Chest pain, trouble breathing, or bloody phlegm produced from a cough should prompt evaluation by a doctor right away
Therefore, phlegm production from the lungs, loss of voice, intestinal symptoms, chest pain or trouble breathing all suggest conditions other than a sinus infection. Chest pain, trouble breathing, or bloody phlegm produced from a cough should prompt evaluation by a doctor right away
In the same way that many colds are inappropriately referred to as a sinus infection, sinus infections can be inappropriately confused with an unusually persistent cold. It is unusual for the common cold to last beyond 10-14 days. Instead, since sinusitis often follows the common cold, cold-like symptoms that persist beyond 2 weeks often represent sinusitis. In fact, acute sinusitis can last for four weeks while chronic sinusitis can last for months. Therefore, any symptoms consistent with a cold or sinusitis that persist beyond two weeks should be evaluated for possible sinusitis.
If you have symptoms of a sinus infection, see your doctor or visit one of CapRock Health’s facilities.
Category: sinusitis
Sinus Pain or Congestion
Is this your child’s symptom?
- Fullness, pressure or pain on the face over a sinus
- Sinus pain occurs above the eyebrow, behind the eye, and under the cheekbone
- Other common symptoms can be a blocked nose, nasal discharge, or postnasal drip
Symptoms
- Most often, the pain or pressure is just on one side of the face.

- Swelling around just one eye.
- Other common symptoms are a stuffy or blocked nose or nasal discharge. Your child may also have a nasal drip down the back of the throat. This is called a postnasal drip.
- Less common symptoms are bad breath or mouth breathing. Also, may have a sore throat and throat clearing from postnasal drip.
- Age Limit. Sinus pain is not a common symptom before 5 years of age.
Causes of Sinus Congestion
- Viral Sinus Infection. Part of the common cold. A cold infects the lining of the nose. It also involves the lining of all the sinuses.
- Bacterial Sinus Infection. A problem when the sinus becomes infected with bacteria. (Occurs in 5% of colds). It starts as a viral sinus infection. Main symptoms are increased sinus pain or return of fever. The skin around the eyelids or cheeks may become red or swollen. Thick nasal secretions that last over 14 days may point to a sinus infection.
 This can occur in younger children.
This can occur in younger children. - Allergic Sinus Reaction. Sinus congestion often occurs with nasal allergies (such as from pollen). Sneezing, itchy nose and clear nasal discharge point to this cause.
Treatment of Sinus Congestion
- Viral Sinus Infection. Nasal washes with saline. Antibiotics are not helpful.
- Bacterial Sinus Infection. Antibiotics by mouth.
- Allergic Sinus Reaction. Treatment of the nasal allergy with allergy medicines also often helps the sinus symptoms.
- All Thick Nasal Drainage. Nasal secretions need treatment with nasal saline when they block the nose. Also, treat if they make breathing through the nose hard. If breathing is noisy, it may mean the dried mucus is farther back. Nasal saline rinses can remove it.
Color of Nasal Discharge with Colds
- The nasal discharge changes color during different stages of a cold.
 This is normal.
This is normal. - It starts as a clear discharge and later becomes cloudy.
- Sometimes it becomes yellow or green colored for a few days. This is still normal.
- Colored discharge is common after sleep, with allergy medicines or with low humidity. Reason: all of these events decrease the amount of normal nasal secretions.
Bacterial Sinus Infections: When to Suspect
- Yellow or green nasal discharge is seen with both viral and bacterial sinus infections. Suspect a bacterial infection if the discharge becomes thick (like pus). But, it also needs one or more of these symptoms:
- Sinus Pain, not just normal sinus congestion. Pain occurs mainly behind the cheekbone or eye or
- Swelling or redness of the skin over any sinus or
- Fever lasts more than 3 days or
- Fever returns after it’s been gone for over 24 hours or
- Nasal discharge and post-nasal drip lasts over 14 days without improvement
When to Call for Sinus Pain or Congestion
Call 911 Now
- Not moving or too weak to stand
- Severe trouble breathing (struggling for each breath, can barely speak or cry)
- You think your child has a life-threatening emergency
Call Doctor or Seek Care Now
- Trouble breathing, but not severe.
 Exception: gone after cleaning out the nose.
Exception: gone after cleaning out the nose. - Redness or swelling on the cheek, forehead or around the eye
- Severe headache and getting worse
- Severe pain and not better after using care advice
- Weak immune system. Examples are: sickle cell disease, HIV, cancer, organ transplant, taking oral steroids.
- Fever over 104° F (40° C)
- Your child looks or acts very sick
- You think your child needs to be seen, and the problem is urgent
Contact Doctor Within 24 Hours
- Headache lasts more than 48 hours
- Fever lasts more than 3 days
- Fever returns after being gone more than 24 hours
- Earache occurs
- Sinus pain (not just pressure) and fever
- You think your child needs to be seen, but the problem is not urgent
Contact Doctor During Office Hours
- Sinus pain (not just pressure or fullness) lasts more than 24 hours, after using nasal washes
- Thick yellow or green pus draining from nose and not improved by nasal washes.
 Exception: yellow or green tinged secretions are normal.
Exception: yellow or green tinged secretions are normal. - Sinus congestion and fullness lasts more than 14 days
- Nasal discharge lasts more than 2 weeks
- You have other questions or concerns
Self Care at Home
- Normal sinus congestion as part of a cold
Seattle Children’s Urgent Care Locations
If your child’s illness or injury is life-threatening, call 911.
-
Bellevue
-
Everett
-
Federal Way
-
Seattle
-
Virtual Urgent Care
Care Advice for Sinus Congestion
- What You Should Know About Sinus Congestion:
- Sinus congestion is a normal part of a cold.

- Nasal discharge normally changes color during different stages of a cold. It starts as clear, then cloudy, turns yellow-green tinged, then dries up.
- Yellow or green-tinged discharge. This is more common with sleep, antihistamines or low humidity. (Reason: decrease the amount of normal nasal secretions.)
- Usually, nasal washes can prevent a bacterial sinus infection.
- Antibiotics are not helpful for the sinus congestion that occurs with colds.
- Here is some care advice that should help.
- Sinus congestion is a normal part of a cold.
- Nasal Saline to Open a Blocked Nose:
- Use saline (salt water) nose spray (such as store brand). This helps to loosen up the dried mucus. If you don’t have saline, you can use a few drops of water. Use bottled water, distilled water or boiled tap water. Teens can just splash a little water in the nose and then blow.
- Step 1: Put 3 drops in each nostril.
- Step 2: Blow each nostril out while closing off the other nostril.
 Then, do the other side.
Then, do the other side. - Step 3: Repeat nose drops and blowing until the discharge is clear.
- How often: Do saline rinses when your child can’t breathe through the nose.
- Saline nose drops or spray can be bought in any drugstore. No prescription is needed.
- Reason for nose drops: Suction or blowing alone can’t remove dried or sticky mucus.
- Other option: use a warm shower to loosen mucus. Breathe in the moist air, then blow each nostril.
- Fluids – Offer More:
- Try to get your child to drink lots of fluids.
- Goal: Keep your child well hydrated.
- It also will thin out the mucus discharge from the nose.
- It also loosens up any phlegm in the lungs. Then it’s easier to cough up.
- Humidifier:
- If the air in your home is dry, use a humidifier. Reason: Dry air makes nasal mucus thicker.
- Decongestant Nose Spray (Age 12 years or Older):
- Use this only if the sinus still seems blocked up after nasal washes.
 Use the long-acting type (such as Afrin).
Use the long-acting type (such as Afrin). - Dose: 1 spray on each side. Do this 2 times per day.
- Always clean out the nose with saline before using.
- Use for 1 day. After that, use only for symptoms.
- Don’t use for more than 3 days. (Reason: Can cause rebound congestion).
- Decongestants given by mouth (such as Sudafed) are another choice. They can also open a stuffy nose and ears. Side effects: They may make a person feel nervous or dizzy. Follow the package directions.
- Use this only if the sinus still seems blocked up after nasal washes.
- Pain Medicine:
- To help with the pain, give an acetaminophen product (such as Tylenol).
- Another choice is an ibuprofen product (such as Advil).
- Use as needed.
- Try saline first. Sometimes it alone relieves the pain.
- Cold Pack for Pain:
- For pain or swelling, use a cold pack. You can also use ice wrapped in a wet cloth.
- Put it over the sinus for 20 minutes.
- Caution: Avoid frostbite.

- Allergy Medicine:
- If the child also has nasal allergies, give an allergy medicine.
- Long-acting allergy medicines (such as Zyrtec) are best. Reason: these meds do not cause your child to act sleepy. Age limit: 2 and older.
- A single dose of Benadryl can be given for any breakthrough symptoms.
- No prescription is needed. Age limit: 1 and older.
- What to Expect:
- With this advice, the viral sinus blockage goes away in 7 to 14 days.
- The main problem is a sinus infection from bacteria. This can occur if bacteria multiply within the blocked sinus. This leads to a fever and increased pain. It needs antibiotics. Once on treatment, the symptoms will improve in a few days.
- Return to School:
- Sinus infections cannot be spread to others.
- Your child can return to school after the fever is gone. Your child should feel well enough to join in normal activities.

- Call Your Doctor If:
- Sinus pain lasts more than 24 hours after starting treatment
- Sinus congestion lasts more than 2 weeks
- Fever lasts more than 3 days
- You think your child needs to be seen
- Your child becomes worse
And remember, contact your doctor if your child develops any of the ‘Call Your Doctor’ symptoms.
Disclaimer: this health information is for educational purposes only. You, the reader, assume full responsibility for how you choose to use it.
Last Reviewed: 07/17/2023
Last Revised: 12/30/2022
Copyright 2000-2023. Schmitt Pediatric Guidelines LLC.
Sine theorem. Formulas and Proofs
Let’s help you understand and love math
Start learning
159.4K
Railroad tracks are parallel to each other, and trees grow at an angle to the ground. Alas, with the ratio of the sides in a triangle, everything is not so simple: to determine them, you need the sine theorem.
Proof of the sine theorem
The sine theorem is as follows: the sides of a triangle are proportional to the sines of the opposite angles.
Draw a standard triangle and write the theorem with the formula:
Formula of the sine theorem:
Prove the theorem using the triangle area formula in terms of the sine of its angle.
From this formula we get two ratios:
On b we reduce, we use the rule of proportion and get:
From these two relations we get:
The sine theorem for the triangle is proved.
This theorem is useful to find:
The sides of a triangle given two angles and one side.

Angles of a triangle, given two sides and one included angle.
Find out what professions of the future will suit you
Take the test and we will show you who you can become, and we will also send you a detailed guide on how to realize yourself right now
Proof of the corollary of the sine theorem
The sine theorem has an important consequence. Let’s draw a triangle, describe a circle around it and consider the consequence through the radius.
, where R is the radius of the circle circumscribed about the triangle.
This is how three formulas for the radius of the circumscribed circle were formed:
The main meaning of the corollary of the sine theorem lies in this formula:
The doubled radius of the circumscribed circle is equal to the ratio of the side of the triangle to the sine of the opposite angle.
To prove the corollary of the sine theorem, consider three cases.
1. The angle ∠A = α is acute in triangle ABC.
Draw diameter BA 1 . In this case, point A and point A 1 lie in the same half-plane from the line BC.
Using the inscribed angle theorem, we see that ∠А = ∠А 1 = α. The triangle BA 1 C is right-angled, in it ∠ BCA 1 = 90°, since it rests on the diameter BA 1 .
To find leg a in triangle BA 1 C, multiply the hypotenuse BA 1 by the sine of the opposite angle.
BA 1 = 2R, where R is the radius of the circle
Therefore:
For an acute triangle with a circumscribed circle, the theorem is proved.
2. The angle ∠A = α is obtuse in triangle ABC.
The angle ∠A = α is obtuse in triangle ABC.
Draw the diameter of the circle BA 1 . Points A and A 1 on opposite sides of the straight line BC. Quadrilateral ACA 1 B is inscribed in a circle, and its main property is that the sum of opposite angles is 180°.
Therefore, ∠А 1 = 180° – α.
Recall the property of a quadrilateral inscribed in a circle:
It is also known that sin(180° – α) = sinα.
In triangle BCA 1 , the vertex angle C is 90° because it rests on the diameter. Therefore, we find the leg and in this way:
α \u003d 2R sin (180 ° – α) \u003d 2R sinα
Therefore:
For an obtuse triangle with a circumscribed circle, the theorem is proved.
Commonly used obtuse corners:
3. Angle ∠A = 90°.
Angle ∠A = 90°.
In rectangle ABC, angle A is right, and the opposite side is BC = α = 2R, where R is the radius of the circumscribed circle.
Therefore:
For a right triangle with a circumscribed circle, the theorem is proved.
For those who want to connect their lives with the exact sciences, Skysmart offers courses in specialized mathematics.
Examples of problem solving
The sine theorem and its consequences are actively used in problem solving. Let’s look at a few examples to reinforce the material.
Example 1. In triangle ABC ∠A = 45°, ∠C = 15°, BC = 4√6. Find AC.
How to solve:
According to the triangle sum of angles theorem:
∠A + ∠B + ∠C = 180°
∠B = 180° – 45° – 15° = 120°
Find the AC side using the sine theorem:
Answer: AC = 12.
Example 2. The hypotenuse and one of the legs of a right triangle are 10 and 8 cm, respectively. Find the angle opposite the given leg.
How we solve:
Let’s take the unknown angle as x. Then the aspect ratio looks like this:
Therefore:
So .
Answer: The angle is approximately 53.1°.
Memorize
The usual theorem: The sides of a triangle are proportional to the sines of the opposite angles.
Extended theorem: in an arbitrary triangle, the following relation holds:
, where R is the radius of the circumscribed circle around the triangle.
Math cheat sheets for parents
All math formulas at hand
Lidia Kazantseva
By Skysmart
To the previous article
386. 7K
7K
9 0235 Places and classes of numbers
To the next article
235.1K
Direct and inverse proportionality
Get a learning plan that will help you understand and love math
At an introductory lesson with a tutor learning
Let’s tell you how the classes are going
Let’s choose a course
The theorem of cosines and sines of a triangle. Formulas and examples
We will help you understand and love mathematics
Start learning
262.2K
Grade 9 is a time full of new knowledge. In order not to get confused in the geometry theory, we recommend making cards with information on each topic. In this article you will find the most important thing about the cosine theorem.
Formulation and proof of the cosine theorem
First, let’s recall the Pythagorean theorem: in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.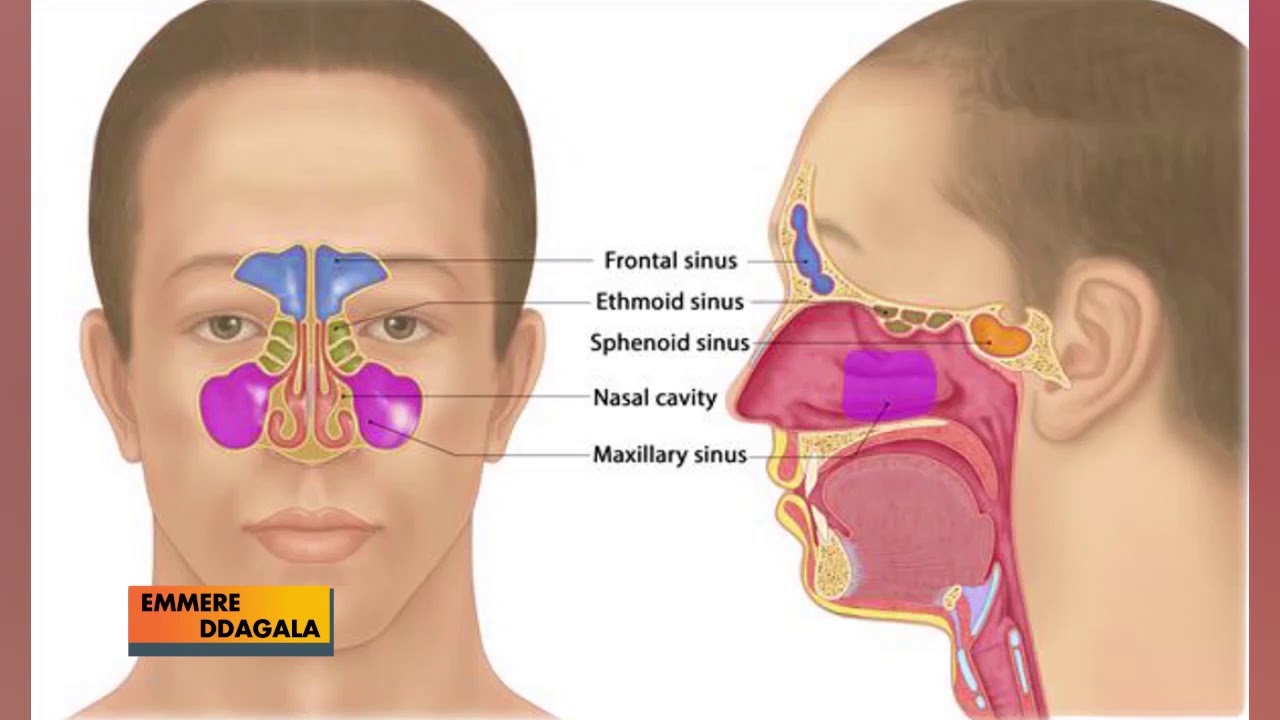
Formula Pythagoras :
a 2 > + b 2 > = c 2 >, where a, b are legs, c is the hypotenuse.
The cosine theorem reads as follows: the square of a side of a triangle is equal to the sum of the squares of its other two sides minus twice the product of these sides by the cosine of the angle between them. Cosine formula: a 2 = b 2 + c 2 – 2bc cos α |
In proof of the cosine theorem we use the formula for the length of a segment in coordinates. Consider this formula:
BC 2 = (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
In the proof of the BC cosine theorem is the side of the triangle ABC, which is denoted by the letter a. We introduce a convenient coordinate system and find the coordinates of the points we need. Point B has coordinates (c; 0).
We introduce a convenient coordinate system and find the coordinates of the points we need. Point B has coordinates (c; 0).
Coordinates of point С — (b cos α; b sin α) for α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 – basic trigonometric identity.
BC 2 = a 2 = (b cos α – c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α – 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) – 2bc cos α + c 2
What was required to be proved.
Tip: to get to grips with a complex topic faster, sign up for
online courses in mathematics for children and teenagers.
Using the law of cosines, you can find the cosine of the angle of a triangle:
- 0285 > 0, the angle α will be acute.

- When b 2 + c 2 – a 2 = 0, angle α will be right.
- When b 2 + c 2 – a 2 < 0, the angle α will be obtuse.
Memorize
When the angle α is straight, then the cosine theorem turns into the Pythagorean theorem.
Let’s formulate another proof of the cosine theorem .
Let us be given a triangle ABC in which height CD is lowered from vertex C to side AB. This means:
- AD = b × cos α,
- DB = c – b × cos α.
Write the Pythagorean theorem for two right triangles ADC and BDC:
- h 2 = b 2 – (b × cos α) 2
- h 2 = a 2 – (c – b × cos α) 2
Equate the right sides of the equations:
- b 2 – (b × cos α) 2 = a 2 – (c – b × cos α) 2 9003 2
or
- a 2 = b 2 + c 2 – 2bc × cos α
If one of the corners at the base is obtuse (the height rests on the continuation of the base), it is completely similar to that considered above.
Define sides b and c:
- b 2 = a 2 + c 2 – 2ac × cos β;
- c 2 = a 2 + b 2 – 2ab × cos γ.
Solve your math homework for 5.
Detailed solutions will help you understand the most difficult topic.
Statement of the theorem for each side of the triangle
The cosine theorem is valid for all sides of the triangle, i.e.: a
b 2 = c 2 + a 2 – 2ca cos β s γ
The cosine theorem can be used for any kind of triangle .
Cosines of the angles of a triangle
The cosine theorem allows you to find both the cosine and the angle of a triangle. Let’s find the cosines of the angles:
Similarly:
Determination of the angle using the cosine
And now let’s pay attention to the angles.
As we already know, the cosine of an angle from the interval (0°; 180°) determines the angle (as opposed to its sine).
Let us be given a unit semicircle. If we are given cos α, then we are given a point on the upper semicircle and an angle α is given. Therefore, cos α uniquely determines the point M(cos α; sin α), and the angle ∠AOM is uniquely determined.
Consideration of the limits of variation of cos α and sin α
Consider the limits of variation of sine and cosine α. Recall that if α is the angle of a triangle, then it lies between 0° and 180°.
Limit of cosine change: -1 < cos α < 1.
Limit of change of sine: 0 < sin α ≤ 1.
- If cos α > 0, then α ∈ ( 0°;90° )
- If cos α < 0, then α ∈ (90°;180°)
- If cos α = 0, then α = 90°
Examples of solving problems
Using the cosine theorem, you can solve geometry problems. Let’s consider some interesting cases.
Let’s consider some interesting cases.
Example 1. Triangle ABC is given. Find the length CM.
∠C = 90°, AB = 9, BC = 3, AM/MB = 1/2, where M is a point on the hypotenuse of AB.
How do we decide:
- Since AM + MB = 9, and AM / MB = 1/2, then AM = 3, MB = 6.
From the triangle ABC we find cos B: - From the triangle CMB by the cosine theorem we find the SM:
Answer: CM = .
Example 2. Given a triangle ABC, in which a 2 + b 2 < c 2 . Prove that ∠C is an obtuse angle.
How to prove:
- Since a 2 + b 2 < c 2 , then cos C < 0, hence ∠C is obtuse.


 This can occur in younger children.
This can occur in younger children. This is normal.
This is normal. Exception: gone after cleaning out the nose.
Exception: gone after cleaning out the nose. Exception: yellow or green tinged secretions are normal.
Exception: yellow or green tinged secretions are normal.
 Use the long-acting type (such as Afrin).
Use the long-acting type (such as Afrin).



