Sinus one side. Sinus Pain on One Side: Causes, Symptoms, and Treatment Options
What are the common causes of sinus pain on one side. How can you differentiate between viral and bacterial sinus infections. When should you seek medical attention for sinus congestion. What are effective home remedies for sinus pain relief.
Understanding Sinus Pain and Congestion
Sinus pain and congestion can be uncomfortable and disruptive to daily life. When these symptoms occur on only one side of the face, it can be particularly concerning. This article will explore the causes, symptoms, and treatment options for unilateral sinus pain and congestion.
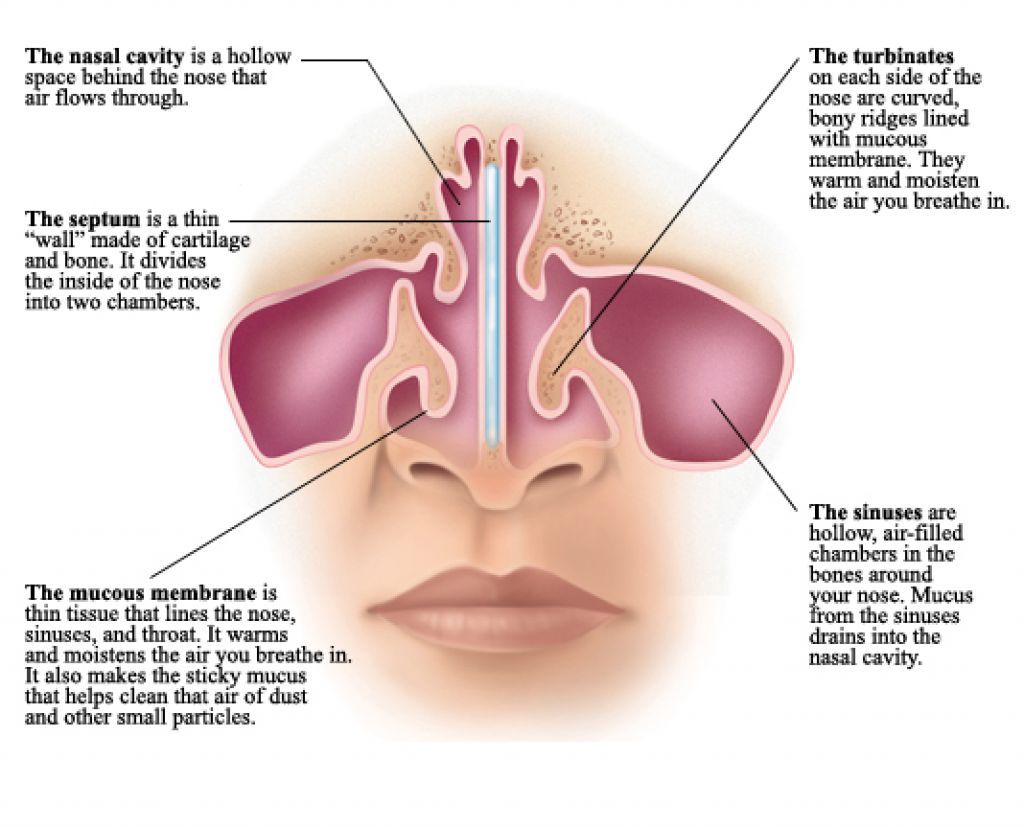
What are sinuses?
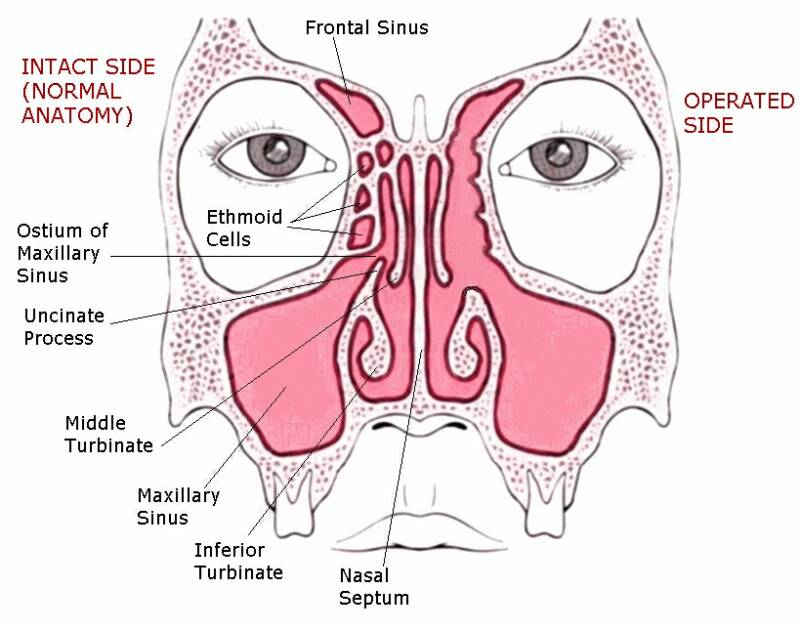
Sinuses are air-filled cavities located in the facial bones surrounding the nose. There are four pairs of sinuses:
- Frontal sinuses (above the eyebrows)
- Maxillary sinuses (behind the cheekbones)
- Ethmoid sinuses (between the eyes)
- Sphenoid sinuses (behind the eyes)
These sinuses play a crucial role in filtering and humidifying the air we breathe, as well as producing mucus to trap harmful particles.

Common Symptoms of Sinus Pain and Congestion
Sinus pain and congestion can manifest in various ways. Understanding these symptoms can help in identifying the underlying cause and seeking appropriate treatment.
Primary symptoms of sinus issues
- Fullness, pressure, or pain over a sinus area
- Pain above the eyebrow, behind the eye, or under the cheekbone
- Blocked or stuffy nose
- Nasal discharge
- Postnasal drip (mucus dripping down the back of the throat)
Additional symptoms that may occur
- Swelling around one eye
- Bad breath
- Mouth breathing
- Sore throat
- Frequent throat clearing
It’s important to note that sinus pain is not a common symptom in children under 5 years of age.
Causes of Sinus Congestion and Pain on One Side
Understanding the underlying causes of sinus congestion and pain is crucial for effective treatment. There are several potential reasons why you might experience these symptoms on one side of your face.
Viral Sinus Infection
A viral sinus infection is often part of the common cold. It affects the lining of the nose and all the sinuses. Symptoms typically include:

- Nasal congestion
- Clear or cloudy nasal discharge
- Mild facial pressure or discomfort
- Low-grade fever
Bacterial Sinus Infection
Bacterial sinus infections occur in about 5% of colds when bacteria infect the sinuses. Key indicators include:
- Increased sinus pain or pressure
- Return of fever after initial improvement
- Redness or swelling around the eyes or cheeks
- Thick, colored nasal discharge lasting over 14 days
Allergic Sinus Reaction
Allergies can cause sinus congestion, often accompanied by:
- Sneezing
- Itchy nose
- Clear nasal discharge
- Watery eyes
Diagnosing Sinus Infections: Viral vs. Bacterial
Distinguishing between viral and bacterial sinus infections is crucial for proper treatment. While both can cause similar symptoms, there are key differences to look out for.
How can you tell if a sinus infection is viral or bacterial?
Viral sinus infections typically:
- Improve within 7-10 days
- Start with clear nasal discharge that may become cloudy
- Cause mild to moderate facial discomfort
Bacterial sinus infections often:
- Persist for more than 10 days without improvement
- Worsen after initial improvement (double worsening)
- Cause severe facial pain, especially on one side
- Produce thick, colored nasal discharge for more than 3-4 days
Is colored nasal discharge always a sign of bacterial infection?
Contrary to popular belief, the color of nasal discharge alone is not a reliable indicator of a bacterial infection. Both viral and bacterial infections can cause clear, cloudy, or colored discharge. The duration and severity of symptoms are more important factors in distinguishing between the two.
Treatment Options for Sinus Congestion and Pain
The appropriate treatment for sinus congestion and pain depends on the underlying cause. Here are some common approaches:
Viral Sinus Infection Treatment
- Nasal saline rinses or sprays to clear congestion
- Over-the-counter pain relievers for discomfort
- Rest and hydration
- Humidifiers to moisten the air
Antibiotics are not effective against viral infections and should be avoided.

Bacterial Sinus Infection Treatment
- Antibiotics prescribed by a healthcare provider
- Nasal decongestants (short-term use only)
- Pain relievers for discomfort
- Nasal saline rinses
Allergic Sinus Reaction Treatment
- Antihistamines to reduce allergy symptoms
- Nasal corticosteroid sprays to decrease inflammation
- Allergy shots for long-term management
- Avoiding known allergens
Home Remedies for Sinus Pain Relief
In addition to medical treatments, several home remedies can help alleviate sinus pain and congestion:
- Steam inhalation: Inhaling steam from a bowl of hot water or a warm shower can help moisturize the sinuses and loosen mucus.
- Nasal irrigation: Using a neti pot or saline nasal spray can help flush out irritants and thin mucus.
- Warm compress: Applying a warm, damp towel to the face can help relieve pain and pressure.
- Hydration: Drinking plenty of water helps thin mucus and promote drainage.
- Elevating the head: Sleeping with your head slightly elevated can improve sinus drainage.
When to Seek Medical Attention for Sinus Issues
While many sinus problems can be managed at home, certain symptoms warrant medical attention. Knowing when to seek help is crucial for preventing complications and ensuring proper treatment.

Symptoms requiring immediate medical care (call 911)
- Severe difficulty breathing
- Inability to move or extreme weakness
- Any symptoms that suggest a life-threatening emergency
Symptoms requiring prompt medical attention
- Redness or swelling on the cheek, forehead, or around the eye
- Severe headache that’s worsening
- Fever over 104°F (40°C)
- Symptoms in individuals with weakened immune systems
Symptoms requiring a doctor’s appointment
- Sinus pain lasting more than 24 hours despite home treatment
- Fever lasting more than 3 days or returning after being gone for 24 hours
- Thick, colored nasal discharge lasting more than 14 days
- Sinus congestion and fullness persisting for more than 2 weeks
Preventing Sinus Infections and Congestion
While it’s not always possible to prevent sinus issues, certain measures can reduce your risk:
- Practice good hand hygiene to avoid viral infections
- Stay hydrated to keep nasal passages moist
- Use a humidifier in dry environments
- Avoid known allergens and irritants
- Quit smoking and avoid secondhand smoke
- Manage allergies with appropriate medications
By understanding the causes, symptoms, and treatment options for sinus pain and congestion, you can better manage these uncomfortable conditions. Remember to consult with a healthcare provider if symptoms persist or worsen, especially if they primarily affect one side of your face. With proper care and attention, most sinus issues can be effectively treated, allowing you to breathe easier and feel more comfortable.

Sinus Pain or Congestion
Is this your child’s symptom?
- Fullness, pressure or pain on the face over a sinus
- Sinus pain occurs above the eyebrow, behind the eye, and under the cheekbone
- Other common symptoms can be a blocked nose, nasal discharge, or postnasal drip
Symptoms
- Most often, the pain or pressure is just on one side of the face.
- Swelling around just one eye.
- Other common symptoms are a stuffy or blocked nose or nasal discharge. Your child may also have a nasal drip down the back of the throat. This is called a postnasal drip.
- Less common symptoms are bad breath or mouth breathing. Also, may have a sore throat and throat clearing from postnasal drip.
- Age Limit. Sinus pain is not a common symptom before 5 years of age.
Causes of Sinus Congestion
- Viral Sinus Infection. Part of the common cold. A cold infects the lining of the nose. It also involves the lining of all the sinuses.

- Bacterial Sinus Infection. A problem when the sinus becomes infected with bacteria. (Occurs in 5% of colds). It starts as a viral sinus infection. Main symptoms are increased sinus pain or return of fever. The skin around the eyelids or cheeks may become red or swollen. Thick nasal secretions that last over 14 days may point to a sinus infection. This can occur in younger children.
- Allergic Sinus Reaction. Sinus congestion often occurs with nasal allergies (such as from pollen). Sneezing, itchy nose and clear nasal discharge point to this cause.
Treatment of Sinus Congestion
- Viral Sinus Infection. Nasal washes with saline. Antibiotics are not helpful.
- Bacterial Sinus Infection. Antibiotics by mouth.
- Allergic Sinus Reaction. Treatment of the nasal allergy with allergy medicines also often helps the sinus symptoms.
- All Thick Nasal Drainage.
 Nasal secretions need treatment with nasal saline when they block the nose. Also, treat if they make breathing through the nose hard. If breathing is noisy, it may mean the dried mucus is farther back. Nasal saline rinses can remove it.
Nasal secretions need treatment with nasal saline when they block the nose. Also, treat if they make breathing through the nose hard. If breathing is noisy, it may mean the dried mucus is farther back. Nasal saline rinses can remove it.
Color of Nasal Discharge with Colds
- The nasal discharge changes color during different stages of a cold. This is normal.
- It starts as a clear discharge and later becomes cloudy.
- Sometimes it becomes yellow or green colored for a few days. This is still normal.
- Colored discharge is common after sleep, with allergy medicines or with low humidity. Reason: all of these events decrease the amount of normal nasal secretions.
Bacterial Sinus Infections: When to Suspect
- Yellow or green nasal discharge is seen with both viral and bacterial sinus infections. Suspect a bacterial infection if the discharge becomes thick (like pus). But, it also needs one or more of these symptoms:
- Sinus Pain, not just normal sinus congestion.
 Pain occurs mainly behind the cheekbone or eye or
Pain occurs mainly behind the cheekbone or eye or - Swelling or redness of the skin over any sinus or
- Fever lasts more than 3 days or
- Fever returns after it’s been gone for over 24 hours or
- Nasal discharge and post-nasal drip lasts over 14 days without improvement
When to Call for Sinus Pain or Congestion
Call 911 Now
- Not moving or too weak to stand
- Severe trouble breathing (struggling for each breath, can barely speak or cry)
- You think your child has a life-threatening emergency
Call Doctor or Seek Care Now
- Trouble breathing, but not severe. Exception: gone after cleaning out the nose.
- Redness or swelling on the cheek, forehead or around the eye
- Severe headache and getting worse
- Severe pain and not better after using care advice
- Weak immune system. Examples are: sickle cell disease, HIV, cancer, organ transplant, taking oral steroids.
- Fever over 104° F (40° C)
- Your child looks or acts very sick
- You think your child needs to be seen, and the problem is urgent
Contact Doctor Within 24 Hours
- Headache lasts more than 48 hours
- Fever lasts more than 3 days
- Fever returns after being gone more than 24 hours
- Earache occurs
- Sinus pain (not just pressure) and fever
- You think your child needs to be seen, but the problem is not urgent
Contact Doctor During Office Hours
- Sinus pain (not just pressure or fullness) lasts more than 24 hours, after using nasal washes
- Thick yellow or green pus draining from nose and not improved by nasal washes.
 Exception: yellow or green tinged secretions are normal.
Exception: yellow or green tinged secretions are normal. - Sinus congestion and fullness lasts more than 14 days
- Nasal discharge lasts more than 2 weeks
- You have other questions or concerns
Self Care at Home
- Normal sinus congestion as part of a cold
Seattle Children’s Urgent Care Locations
If your child’s illness or injury is life-threatening, call 911.
-
Bellevue
-
Everett
-
Federal Way
-
Seattle
-
Virtual Urgent Care
Care Advice for Sinus Congestion
- What You Should Know About Sinus Congestion:
- Sinus congestion is a normal part of a cold.

- Nasal discharge normally changes color during different stages of a cold. It starts as clear, then cloudy, turns yellow-green tinged, then dries up.
- Yellow or green-tinged discharge. This is more common with sleep, antihistamines or low humidity. (Reason: decrease the amount of normal nasal secretions.)
- Usually, nasal washes can prevent a bacterial sinus infection.
- Antibiotics are not helpful for the sinus congestion that occurs with colds.
- Here is some care advice that should help.
- Sinus congestion is a normal part of a cold.
- Nasal Saline to Open a Blocked Nose:
- Use saline (salt water) nose spray (such as store brand). This helps to loosen up the dried mucus. If you don’t have saline, you can use a few drops of water. Use bottled water, distilled water or boiled tap water. Teens can just splash a little water in the nose and then blow.
- Step 1: Put 3 drops in each nostril.
- Step 2: Blow each nostril out while closing off the other nostril.
 Then, do the other side.
Then, do the other side. - Step 3: Repeat nose drops and blowing until the discharge is clear.
- How often: Do saline rinses when your child can’t breathe through the nose.
- Saline nose drops or spray can be bought in any drugstore. No prescription is needed.
- Reason for nose drops: Suction or blowing alone can’t remove dried or sticky mucus.
- Other option: use a warm shower to loosen mucus. Breathe in the moist air, then blow each nostril.
- Fluids – Offer More:
- Try to get your child to drink lots of fluids.
- Goal: Keep your child well hydrated.
- It also will thin out the mucus discharge from the nose.
- It also loosens up any phlegm in the lungs. Then it’s easier to cough up.
- Humidifier:
- If the air in your home is dry, use a humidifier. Reason: Dry air makes nasal mucus thicker.
- Decongestant Nose Spray (Age 12 years or Older):
- Use this only if the sinus still seems blocked up after nasal washes.
 Use the long-acting type (such as Afrin).
Use the long-acting type (such as Afrin). - Dose: 1 spray on each side. Do this 2 times per day.
- Always clean out the nose with saline before using.
- Use for 1 day. After that, use only for symptoms.
- Don’t use for more than 3 days. (Reason: Can cause rebound congestion).
- Decongestants given by mouth (such as Sudafed) are another choice. They can also open a stuffy nose and ears. Side effects: They may make a person feel nervous or dizzy. Follow the package directions.
- Use this only if the sinus still seems blocked up after nasal washes.
- Pain Medicine:
- To help with the pain, give an acetaminophen product (such as Tylenol).
- Another choice is an ibuprofen product (such as Advil).
- Use as needed.
- Try saline first. Sometimes it alone relieves the pain.
- Cold Pack for Pain:
- For pain or swelling, use a cold pack. You can also use ice wrapped in a wet cloth.
- Put it over the sinus for 20 minutes.
- Caution: Avoid frostbite.

- Allergy Medicine:
- If the child also has nasal allergies, give an allergy medicine.
- Long-acting allergy medicines (such as Zyrtec) are best. Reason: these meds do not cause your child to act sleepy. Age limit: 2 and older.
- A single dose of Benadryl can be given for any breakthrough symptoms.
- No prescription is needed. Age limit: 1 and older.
- What to Expect:
- With this advice, the viral sinus blockage goes away in 7 to 14 days.
- The main problem is a sinus infection from bacteria. This can occur if bacteria multiply within the blocked sinus. This leads to a fever and increased pain. It needs antibiotics. Once on treatment, the symptoms will improve in a few days.
- Return to School:
- Sinus infections cannot be spread to others.
- Your child can return to school after the fever is gone. Your child should feel well enough to join in normal activities.

- Call Your Doctor If:
- Sinus pain lasts more than 24 hours after starting treatment
- Sinus congestion lasts more than 2 weeks
- Fever lasts more than 3 days
- You think your child needs to be seen
- Your child becomes worse
And remember, contact your doctor if your child develops any of the ‘Call Your Doctor’ symptoms.
Disclaimer: this health information is for educational purposes only. You, the reader, assume full responsibility for how you choose to use it.
Last Reviewed: 07/17/2023
Last Revised: 12/30/2022
Copyright 2000-2023. Schmitt Pediatric Guidelines LLC.
Sinus Pressure – When You Should Worry
309988
4
Are you battling a common cold, agitated by allergies or suffering from a sinus infection? Or, perhaps you’re wondering if your symptoms are a sign of COVID-19. Sinus infections affect 28 million people in the U.S. every year. 1 Read on for a review of sinus symptoms and ways to get relief.
1 Read on for a review of sinus symptoms and ways to get relief.
Sinus trouble: consider the causes
Not only can seasonal allergies or chronic allergies impact the sinuses, but humid air can cause a clogged or stuffy feeling in the nose. An infection—either brief or long-lasting—can also take hold.
Sinusitis ailments are not only a burden for allergy sufferers, they can be a challenge for doctors, too, especially as patients and doctors alike are on high alert for warning signs of a possible COVID-19 infection. Three of the most common causes of sinus symptoms are allergies, viral infections and bacterial infections. But these can be tough to tell apart because of overlapping symptoms.
The lowdown on stressed sinuses
A flare-up of seasonal allergies, called hay fever, causes stuffy noses and irritated sinuses. But allergy sufferers will notice mainly that they have a runny (and sometimes itchy) nose with clear output and itchy, watery eyes. Their symptoms are also often tied to certain times of year and specific allergens like animal dander, dust, pollen or mold.
If you’re plugged up with thick mucus that’s green or yellow, you could have an infection. Sinus infections—whether caused by bacteria or a virus—can also bring along other symptoms like mild headache, fatigue, weakness or a cough. Viruses are far more likely to be the cause of sinus infections. Certain symptoms increase the probably of bacterial sinusitis:
- Persistent sinusitis symptoms for longer than 10 days, especially with “double worsening.” This means symptoms start to improve and then get worse a few days later.
- A fever, especially a high one over 102 ℉.
- Asymmetric pain (one side much worse than the other) in one or more sinus areas. These include under or above the eyes and above the bridge of the nose.
“A bacterial infection could be serious if you’re having a severe or constant headache, neck pain or stiffness, extreme sleepiness or a change in mental state,” says physician Kyon Hood, president, Teladoc Health Medical Group. Some of these symptoms overlap with serious or worsening COVID-19 infections, so it’s important to keep a close eye on any symptoms that may signal low blood-oxygen levels, like persistent pain or pressure in the chest, trouble breathing, new confusion or pale, gray or bluish tone to the skin, lips or nail beds, depending on skin tone. “Also watch out for redness and swelling of the cheek, forehead or around the eyes; or double vision, decreased vision or pain when opening or moving your eyes,” he advises.
“Also watch out for redness and swelling of the cheek, forehead or around the eyes; or double vision, decreased vision or pain when opening or moving your eyes,” he advises.
How Teladoc works
Teladoc gives you best-in-class care from doctors from wherever you are. Access our doctors by phone or video to diagnose, treat and even prescribe medicine if needed for common conditions like allergies, cough, flu, pink eye, rashes, sinus infections, sore throats, stomach bugs, UTI and more. Schedule a visit now to talk to a doctor 24/7 for non-emergency conditions.
Pain in the face for a few days in a row along with worsening symptoms may require treatment, Dr. Hood explains, but noted that determining the difference between a bacterial and viral infection isn’t always clear-cut.
How you can find relief
It’s important to review your sinusitis symptoms and how long you’ve been having them with a physician. Teladoc doctors can help you determine the possible cause of your symptoms, especially if you’re concerned you may have COVID-19.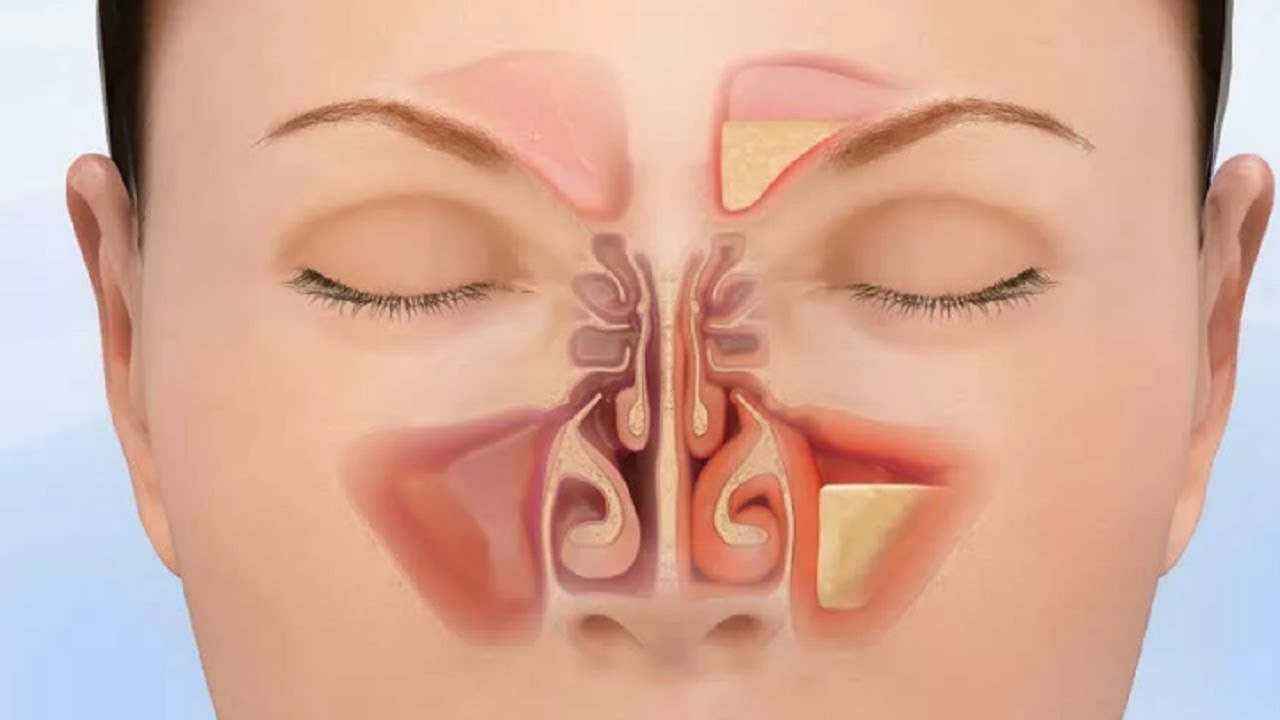 If your sinus problems are caused by allergies, there are strategies and medications that can help bring relief. While bothersome mucus is often an effect of a viral infection, a bacterial infection can develop after a virus has taken hold. In this case, oral antibiotics can help with healing.
If your sinus problems are caused by allergies, there are strategies and medications that can help bring relief. While bothersome mucus is often an effect of a viral infection, a bacterial infection can develop after a virus has taken hold. In this case, oral antibiotics can help with healing.
Regardless of what’s causing all this congestion, try to put the to-do list aside and get some rest. If you’re having pain, you can take an over-the-counter (OTC) pain reliever like acetaminophen or ibuprofen. Petroleum jelly can soothe a sore nose on the outside, while nasal drops or a nasal irrigation device (like the neti pot) can help flush out nasal passages on the inside. “Treat and blow each nostril separately,” Dr. Hood says.
Also, don’t forget about all that mucus you’re losing: Moisture should play a key role in your return to good health. “Drink plenty of liquids like water, juice, warm broth or soup,” Dr. Hood says, “and use a cool-mist humidifier to soothe the airways, especially when sleeping. ” Steam from hot showers can help reduce inflammation and make breathing easier. Also try a warm compress on the nose, cheekbones or forehead for relief from sinusitis symptoms, he adds.
” Steam from hot showers can help reduce inflammation and make breathing easier. Also try a warm compress on the nose, cheekbones or forehead for relief from sinusitis symptoms, he adds.
Pseudoephedrine (also known as Sudafed), an OTC oral decongestant, can help relieve congestion, says Dr. Hood. He notes that certain people—such as those with high blood pressure—must use this medicine with caution. Dr. Hood advises against topical decongestants or nasal sprays such as oxymetazoline (also known as Afrin). “These can cause ‘rebound congestion,’ which actually increases the frequency of runny noses after the medication wears off,” he explains.
Get relief now
Remember that many sinus problems have overlapping symptoms, so it’s best to talk to a Teladoc physician about what’s causing the issue. You can reach out to Teladoc online or by app 24/7 to talk to one of our U.S. board-certified doctors.
Let’s get to the root of the illness so you don’t have to suffer with your sinuses any longer. If you think seasonal allergies may be the cause of your sinusitis symptoms, get fast relief from your allergies today.
If you think seasonal allergies may be the cause of your sinusitis symptoms, get fast relief from your allergies today.
Updated June 9, 2021
1https://www.cdc.gov/nchs/fastats/sinuses.htm
This portion of the Teladoc Health website occasionally offers health, fitness, and nutritional information and is provided for educational purposes only. You cannot rely on any information provided here as a substitute for or replacement of professional medical advice, diagnosis or treatment. Teladoc Health cannot assure that the information contained on this site always includes the most recent findings or developments with respect to the particular subject matter covered.
If you ever have any concerns or questions about your health, you should always consult with a physician or other healthcare professional. Do not disregard, avoid or delay obtaining medical- or health-related advice from your healthcare professional because of something you may have read on this site.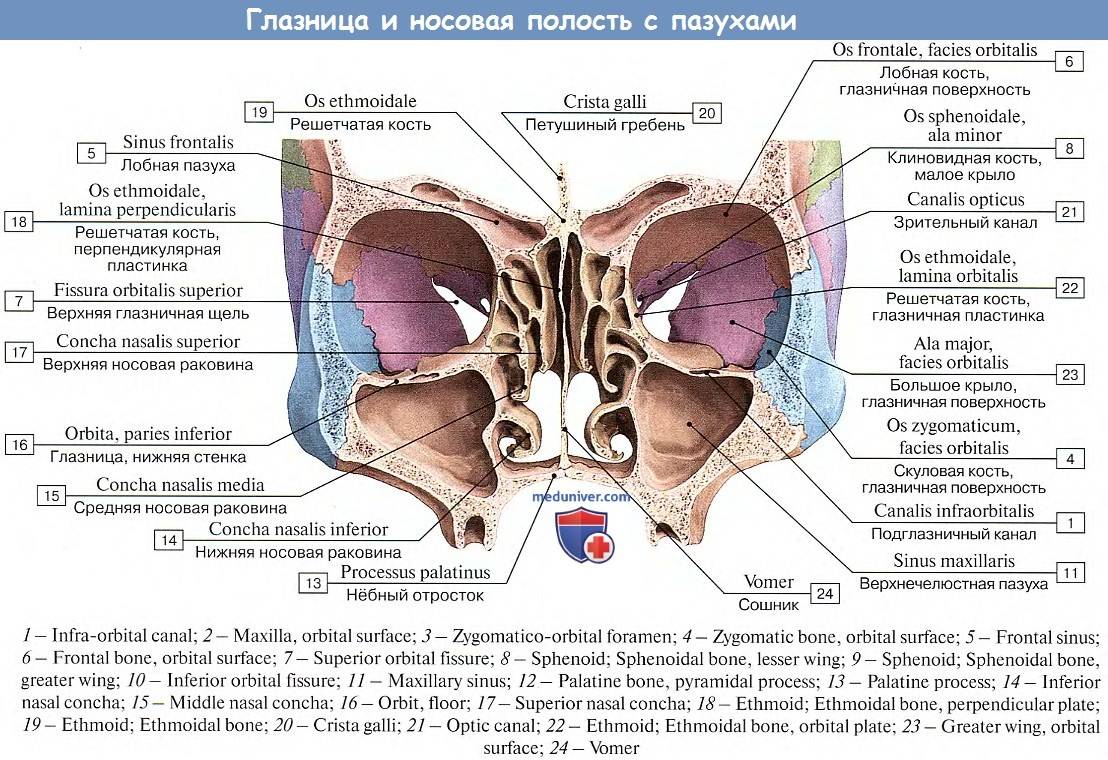 The use of any information provided on this site is solely at your own risk.
The use of any information provided on this site is solely at your own risk.
If you are in the United States and think you are having a medical or health emergency, call your healthcare professional, or 911, immediately.
COVID-19, Health Talk, Sinus
Other stories
Are allergies bad in your state?
Next Story
Spring allergies: Do you have a plan?
Previous Story
Sine theorem. Formulas and Proofs
Let’s help you understand and love math
Start learning
159.4K
Railroad tracks are parallel to each other, and trees grow at an angle to the ground. Alas, with the ratio of the sides in a triangle, everything is not so simple: to determine them, you need the sine theorem.
Proof of the sine theorem
The sine theorem is as follows: the sides of a triangle are proportional to the sines of the opposite angles.
Draw a standard triangle and write the theorem with the formula:
Formula of the sine theorem:
Prove the theorem using the triangle area formula in terms of the sine of its angle.
From this formula we get two ratios:
On b we reduce, we use the rule of proportion and get:
From these two relations we get:
The sine theorem for the triangle is proved.
This theorem is useful to find:
The sides of a triangle given two angles and one side.
Angles of a triangle, given two sides and one included angle.
Find out what professions of the future will suit you
Take the test and we will show you who you can become, and we will also send you a detailed guide on how to realize yourself right now
Proof of the corollary of the sine theorem
The sine theorem has an important consequence.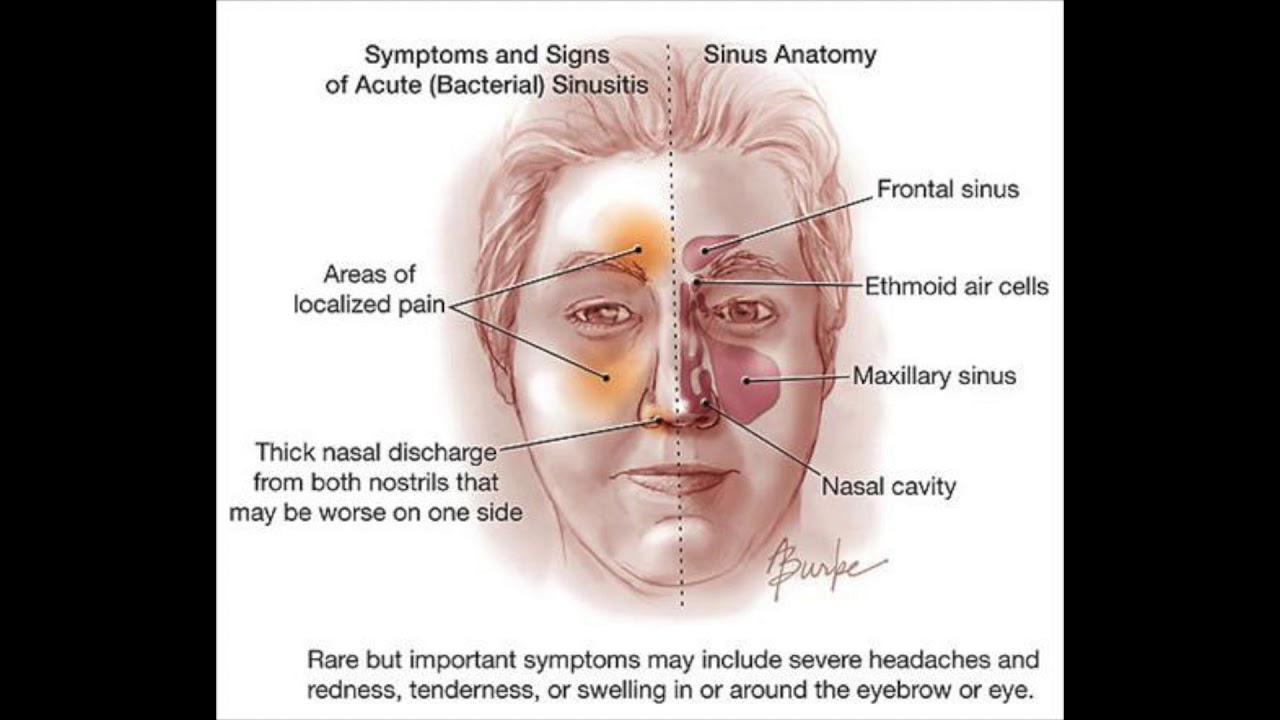 Let’s draw a triangle, describe a circle around it and consider the consequence through the radius.
Let’s draw a triangle, describe a circle around it and consider the consequence through the radius.
, where R is the radius of the circle circumscribed about the triangle.
This is how three formulas for the radius of the circumscribed circle were formed:
The main meaning of the corollary of the sine theorem lies in this formula:
The doubled radius of the circumscribed circle is equal to the ratio of the side of the triangle to the sine of the opposite angle.
To prove the corollary of the sine theorem, consider three cases.
1. The angle ∠A = α is acute in triangle ABC.
Draw diameter BA 1 . In this case, point A and point A 1 lie in the same half-plane from the line BC.
Using the inscribed angle theorem, we see that ∠А = ∠А 1 = α.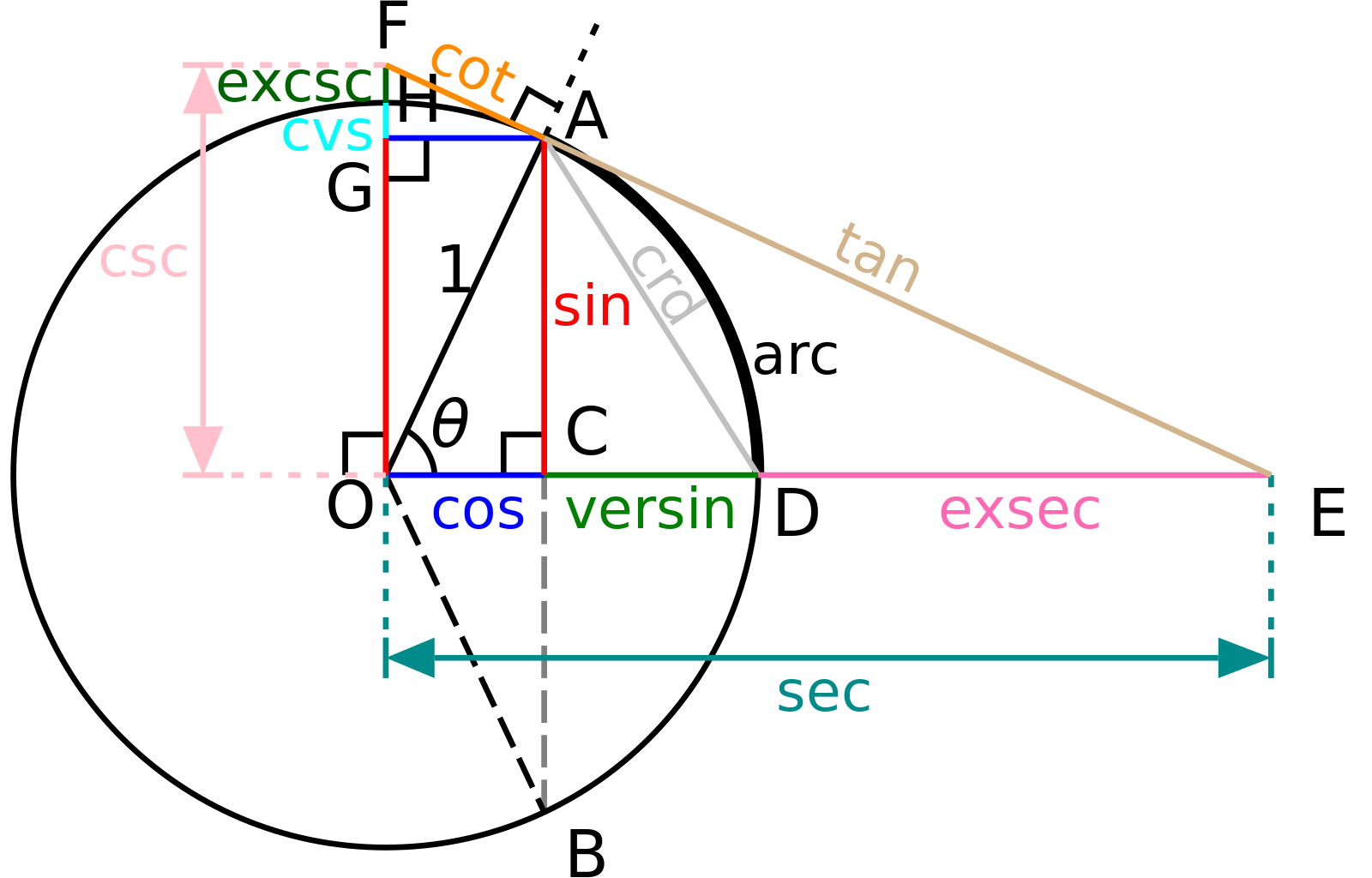 The triangle BA 1 C is right-angled, in it ∠ BCA 1 = 90°, since it rests on the diameter BA 1 .
The triangle BA 1 C is right-angled, in it ∠ BCA 1 = 90°, since it rests on the diameter BA 1 .
To find leg a in triangle BA 1 C, multiply the hypotenuse BA 1 by the sine of the opposite angle.
BA 1 = 2R, where R is the radius of the circle
Therefore:
For an acute triangle with a circumscribed circle, the theorem is proved.
2. The angle ∠A = α is obtuse in triangle ABC.
Draw the diameter of the circle BA 1 . Points A and A 1 on opposite sides of the straight line BC. Quadrilateral ACA 1 B is inscribed in a circle, and its main property is that the sum of opposite angles is 180°.
Therefore, ∠А 1 = 180° – α.
Recall the property of a quadrilateral inscribed in a circle:
It is also known that sin(180° – α) = sinα.
In triangle BCA 1 , the vertex angle C is 90° because it rests on the diameter. Therefore, we find the leg and in this way:
α \u003d 2R sin (180 ° – α) \u003d 2R sinα
Therefore:
For an obtuse triangle with a circumscribed circle, the theorem is proved.
Commonly used obtuse corners:
3. Angle ∠A = 90°.
In rectangle ABC, angle A is right, and the opposite side is BC = α = 2R, where R is the radius of the circumscribed circle.
Therefore:
For a right triangle with a circumscribed circle, the theorem is proved.
For those who want to connect their lives with the exact sciences, Skysmart offers courses in specialized mathematics.
Examples of problem solving
The sine theorem and its consequences are actively used in problem solving. Let’s look at a few examples to reinforce the material.
Example 1. In triangle ABC ∠A = 45°, ∠C = 15°, BC = 4√6. Find AC.
How to solve:
According to the triangle sum of angles theorem:
∠A + ∠B + ∠C = 180°
∠B = 180° – 45° – 15° = 120°
Find the AC side using the sine theorem:
Answer: AC = 12.
Example 2. The hypotenuse and one of the legs of a right triangle are 10 and 8 cm, respectively. Find the angle opposite the given leg.
How we solve:
Let’s take the unknown angle as x.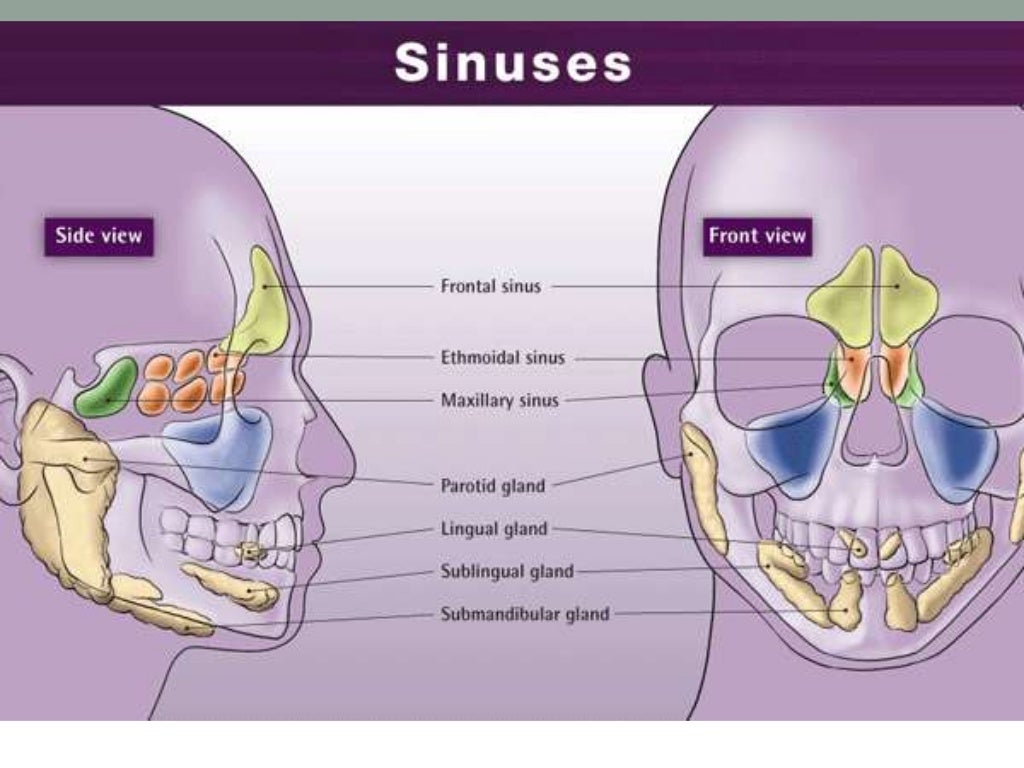 Then the aspect ratio looks like this:
Then the aspect ratio looks like this:
Therefore:
So .
Answer: The angle is approximately 53.1°.
Memorize
The usual theorem: The sides of a triangle are proportional to the sines of the opposite angles.
Extended theorem: in an arbitrary triangle, the following relation holds:
, where R is the radius of the circumscribed circle around the triangle.
Math cheat sheets for parents
All math formulas at hand
Lidia Kazantseva
By Skysmart
To the previous article
386.7K
9 0235 Places and classes of numbers
To the next article
235.1K
Direct and inverse proportionality
Get a learning plan that will help you understand and love math
At an introductory lesson with a tutor learning
Let’s tell you how the classes are going
Let’s choose a course
Sine (sin), cosine (cos), tangent (tg), cotangent (ctg) – how to find, ratio, formulas
We will start studying trigonometry with a right triangle.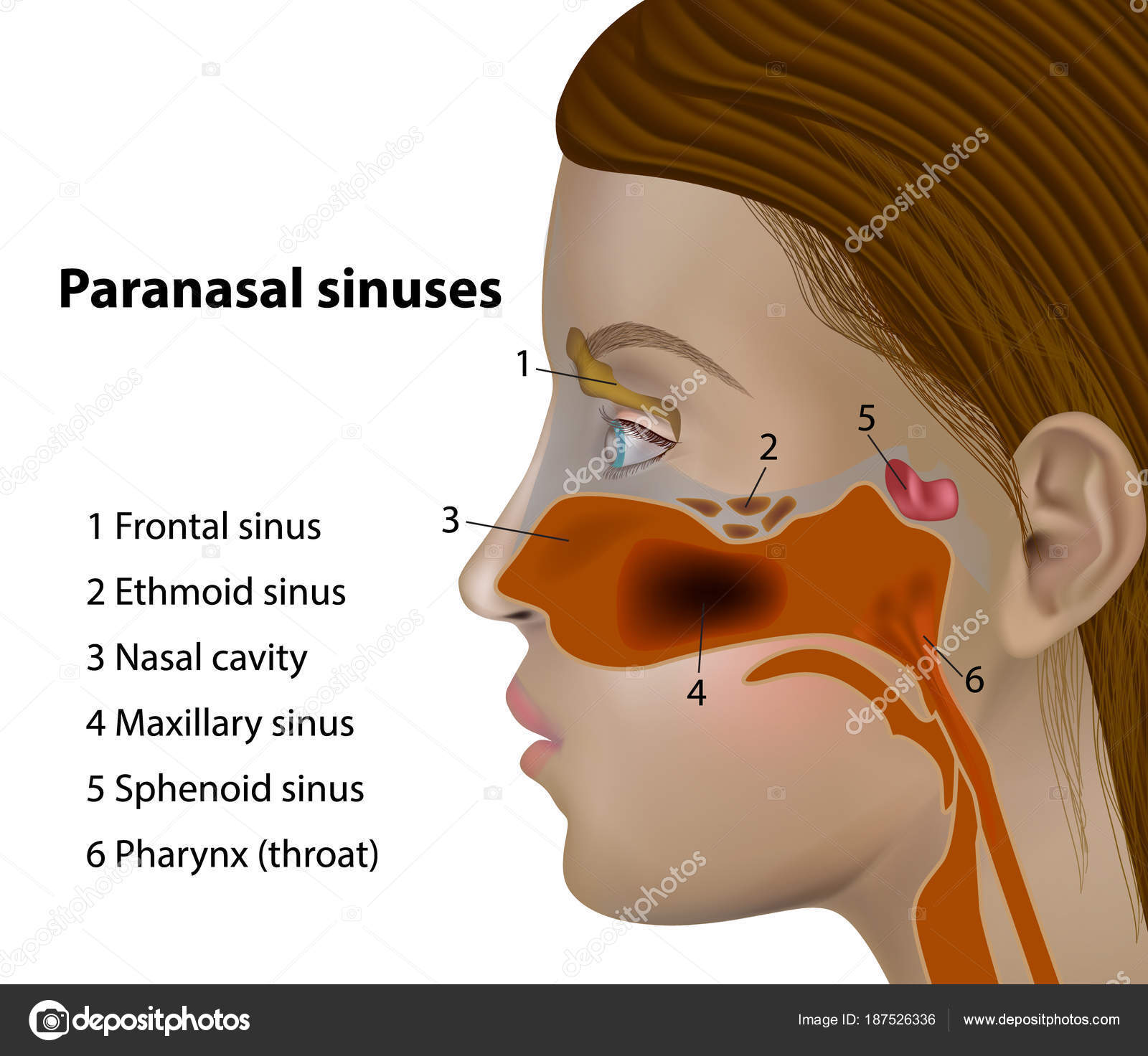 Let’s define what the sine and cosine are, as well as the tangent and cotangent of an acute angle. These are the basics of trigonometry.
Let’s define what the sine and cosine are, as well as the tangent and cotangent of an acute angle. These are the basics of trigonometry.
Recall that is a right angle is an angle equal to 90 degrees. In other words, half of the unfolded corner.
Acute angle – less than 90 degrees.
Obtuse angle – greater than 90 degrees. In relation to such an angle, “obtuse” is not an insult, but a mathematical term 🙂
Let’s draw a right triangle. A right angle is usually denoted C. Note that the side opposite the angle is denoted by the same letter, only lowercase. So, the side lying opposite the angle A is denoted.
Angle A is denoted by the corresponding Greek letter .
The hypotenuse of a right triangle is the side opposite the right angle.
Legs – sides opposite sharp corners.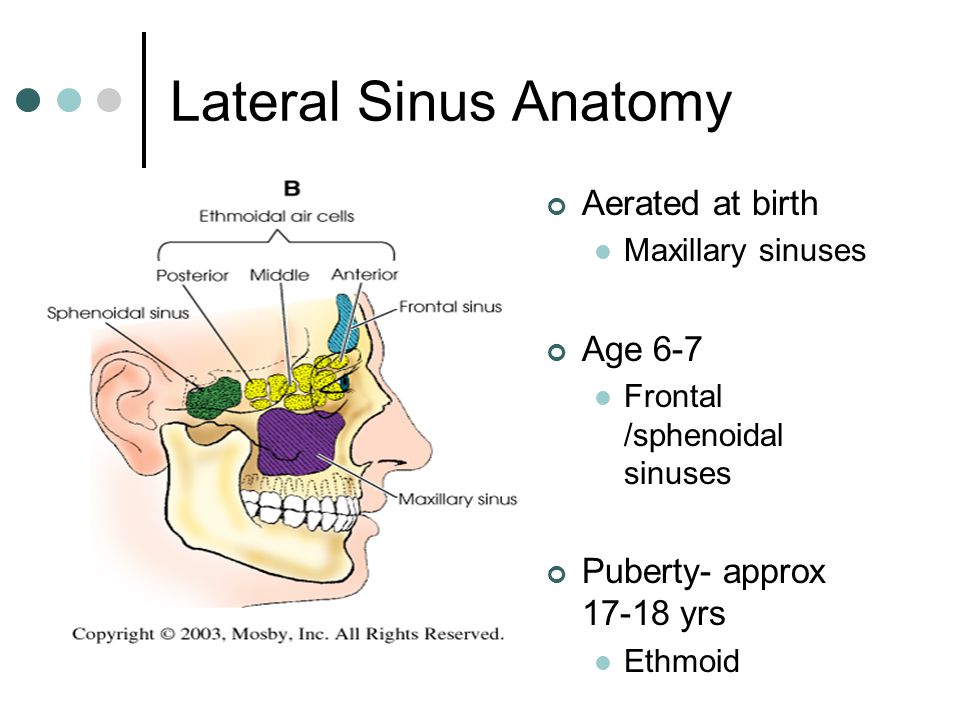
The leg lying opposite the corner is called opposite (in relation to the corner). The other leg, which lies on one side of the corner, is called adjoining .
The sine of an acute angle in a right triangle is the ratio of the opposite leg to the hypotenuse:
sin A
Cosine of an acute angle in a right triangle – ratio of adjacent leg to hypotenuse:
cos A
Tangent of an acute angle in a right triangle – ratio of opposite leg to adjacent:
tg A
Other ( equivalent) definition: the tangent of an acute angle is the ratio of the sine of an angle to its cosine:
tg A
The cotangent of an acute angle in a right triangle is the ratio of the adjacent leg to the opposite one (or, which is the same, the ratio of cosine to sine):
ctg A
Pay attention to the basic formulas for sine, cosine, tangent and cotangent below. They will be useful to us in solving problems.
| sin | sincos | |
| cos | 1+tg | cos = sin |
| tg | 1+ctg | sin = cos |
| ctg | tg = ctg |
Let’s prove some of them.
- The sum of the angles of any triangle is . So the sum of two acute angles of a right triangle is .
- On the one hand, as the ratio of the opposite leg to the hypotenuse. On the other hand, since for the angle the leg and will be adjacent. We get that . In other words, .
- Take the Pythagorean theorem: . Divide both parts by and we get
We have obtained the basic trigonometric identity . - Dividing both parts of the basic trigonometric identity by , we get: This means that if we are given the tangent of an acute angle, then we can immediately find its cosine.
 Likewise,
Likewise,
Well, we have given the definitions and written down the formulas. But why do we need sine, cosine, tangent and cotangent?
We know that the sum of the angles of any triangle is .
We know the ratio between sides right triangle. This is the Pythagorean theorem: .
It turns out that knowing two angles in a triangle, you can find the third one. Knowing two sides in a right triangle, you can find the third. So, for angles – their own ratio, for sides – their own. But what to do if in a right triangle one angle (except for a right one) and one side are known, but you need to find other sides?
This is exactly what people faced in the past, making maps of the area and the starry sky. After all, it is not always possible to directly measure all the sides of a triangle.
The sine, cosine and tangent, also called the trigonometric functions of the angle , give the ratios between the sides and the angles of a triangle. Knowing the angle, you can find all its trigonometric functions using special tables. And knowing the sines, cosines and tangents of the angles of a triangle and one of its sides, you can find the rest.
Knowing the angle, you can find all its trigonometric functions using special tables. And knowing the sines, cosines and tangents of the angles of a triangle and one of its sides, you can find the rest.
We will also draw a table of sine, cosine, tangent and cotangent values for “good” angles from to .
| 0 | |||||
| sin | 0 | ||||
| cos | 0 | ||||
| tg | 0 | – | |||
| ctg | – | 0 |
Pay attention to two dashes in the table. For the corresponding values of the angles, the tangent and cotangent do not exist.
For the corresponding values of the angles, the tangent and cotangent do not exist.
Prove the theorem:
If an acute angle of one right triangle is equal to an acute angle of another right triangle, then the sines of these angles are equal, the cosines of these angles are equal, and the tangents of these angles are equal.
Indeed, let ABC and be two right triangles with right angles C and and equal acute angles A and
Triangles ABC and are similar in the first criterion of similarity of triangles, therefore
From these equalities it follows that i.e. sin A \u003d sin
Similarly, i.e. cos A \u003d cos and i.e. tg A = tg
This means that the sine, cosine and tangent depend only on the magnitude of the angle.
Let’s analyze several problems in trigonometry from the Bank of FIPI tasks.
Problem 1. In triangle ABC, angle C is , sin A = 0.1. Find cos B.
The problem is solved in four seconds.
Since , sin A = cos B = 0.1.
Problem 2. In a triangle, the angle is , , .
Find .
Solution:
Hence
Find AC using the Pythagorean theorem.
Answer: 4.8.
Problem 3. In triangle ABC, angle C is equal to AB = 13, BC = 5. Find the cosine and tangent of acute angle A. Round your answer to the nearest hundredth.
Solution:
For angle A, the opposite leg is BC,
AB is the hypotenuse of the triangle, lies opposite So, sin A
The side adjacent to is AC, therefore, cos A
9 0002 Leg length We will find the AC using the Pythagorean theorem:
Then
cos A
tg A
Answer: 0.92; 0.42.
Note that if the legs of a right triangle are 5 and 12, then the hypotenuse is 13. This is one of the so-called Pythagorean triples. We will talk about them in other articles on the site.
Problem 4. In triangle ABC, angle C is AC = 2, sin A=
In triangle ABC, angle C is AC = 2, sin A=
Find BC.
Solution:
AC = b = 2, BC = a, AB = c.
Since sin A
By the Pythagorean theorem we get
Answer: 0.5.
Problem 5. In triangle ABC, angle C is equal to tg A = Find AB.
Solution:
AC = b = 4, tg A
Answer: 7.
Problem 6.
In triangle ABC, angle C is equal to CH – height, AB = 13, tg A = Find AH.
Solution:
AB = c = 13, tg A = then b = 5a.
According to the Pythagorean theorem ABC:
then
(at two angles), hence whence
Answer: 12.5.
Problem 7. In triangle ABC, angle C is equal to
CH – height, BC = 3, sin A =
Find AH.
Solution:
Since sin A = then c = AB = 18.
sin A = = cos B =
Consider BHC:
= get
then BH = = 0.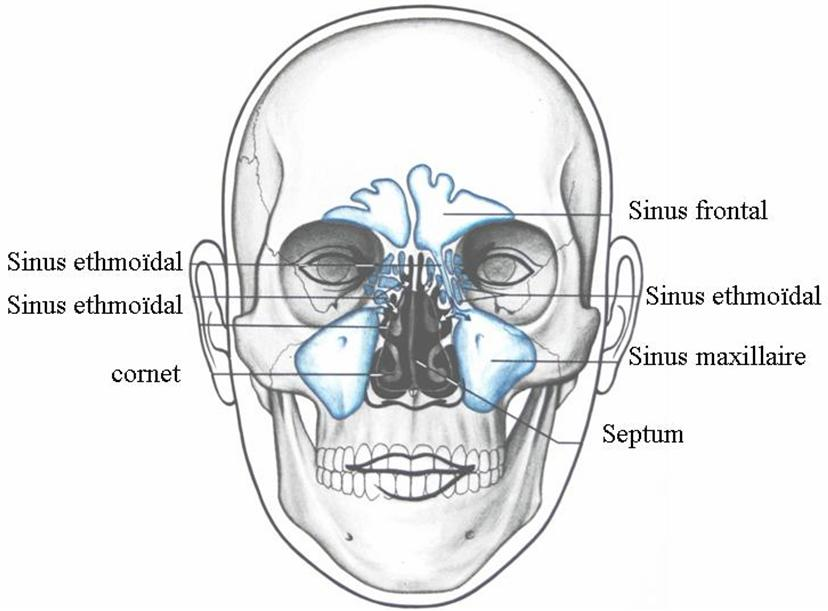 5,
5,
AH = AB – BH = 18 – 0.5 = 17.5.
Answer: 17.5.
Problem 8. In triangle ABC, angle C is equal to 90 CH – height, BC = 3, cos A =
Find AH.
Solution:
Since for ABC: A = sin B =
and for BNS: sin B = = , whence CH =
corner, is the average proportional between the segments into which the hypotenuse is divided by this height. Therefore, for ABC we get:
then
Answer: 17.5.
Problem 9. In triangle ABC, angle C is 90 CH – height, CH = 24 and BH = 7. Find sin A.
Solution:
By definition sin A= = =
,28.
Answer: 0.28.
Problem 10. In triangle ABC, angle C is equal to 90 CH – height, CH = 8 and BH = 4. Find tg A.
Solution:
then tg A = which we find from BHC:
Answer: 0.5.
Problem 11. In triangle ABC, angle C is equal to 90 CH – height, BH = 12, tg A = Find AH.
Solution:
By definition tg A=
Problem 12. In the triangle ABC, the angle C is 90 CH – height, BH = 12, sin A = Find AB.
Solution:
Since cos B = = sin A =
From SVR we have cos B = = then BC =
From ABC we have sinA = = then AB =
Answer: 27.
Problem 13. CH height. Find cos A, AC and AB if CH = 12, BC = 20.
Solution:
3
For ABC: cos A = got cos A = 0.6.
Find AC and AB in several ways.
1st way.
Since cos A = then let AC = 3x, AB = 5x,
then by the Pythagorean theorem we get
x = 5 (since x0). So
2nd way.
(at two corners), then either
k = then AC = ; AB =
3rd method.
(the height of a right triangle drawn from the vertex of the right angle is the average proportional between the segments into which the hypotenuse is divided by this height), then AH = 144:16 = 9.
AB \u003d AN + HB \u003d 9 + 16 \u003d 25.
Using the Pythagorean theorem, we find AC:
\u003d
Answer: cos A \u003d 0.6; AC \u003d 15, AB \u003d 25.
Problem 14.
The height BH of a right triangle ABC drawn from the vertex of right angle B is 24 and cuts off the segment HC from the hypotenuse AC, equal to 18.
Find AB and cos A
Solution:
Using the Pythagorean theorem, we find the hypotenuse BC and cos C from the rectangular VNS:
BC = =
cos C =
0003
Reply : AB = 40, cos A = 0.8.
Problem 15.
The hypotenuse AC of a right triangle ACE is 50, sin A =
Find the area of the triangle.
Solution:
In rectangular ACE sin A =
means = 14.
Find the second leg using the Pythagorean theorem:
16.
In triangle ABC, angle C is right , legs AB = 13 and BC = 12, SK – height.
Find sin Round the result to the nearest hundredth.
Solution:
A-general, ),
means sin
0003
Then sin
The answer is 0.38.
Problem 17. In the triangle ABC AC = BC, AB = 72, cos A = Find the altitude CH.
Solution:
A = that is AC =
By the Pythagorean theorem then
Answer: 15.
Problem 18. In triangle ABC, angle C is 90 sin A = AC = 10 Find AB.
Solution:
1st way.
Since sin A = then we can denote
BC = 11x, AB = 14x.
According to the Pythagorean theorem
(14x-11x)(14x + 11x) = 3 100;
considering that the length of the side is positive, x = 2,
therefore, AB = 14 2 = 28.
2nd way.
Let’s use the basic trigonometric identity
cos A =
By definition, cos A = means
15 Problem 19. Find the angles of the rhombus ABCD , if its diagonals AC and BD are equal to 4 and 4.
Find the angles of the rhombus ABCD , if its diagonals AC and BD are equal to 4 and 4.
Solution:
therefore, in right triangle ABO leg AO \u003d a leg BO \u003d
Therefore tg whence
Answer:
Often in problems there are triangles with angles and or with angles and . Memorize the basic ratios for them by heart!
For a triangle with angles and a leg opposite the angle at , is equal to half of the hypotenuse .
Triangle with angles and is isosceles. In it, the hypotenuse is times larger than the leg.
Problem 20.
In triangle ABC, angle C is equal to 90 angle A is 30 AB = 2
Find the height CH.
Solution:
0003
Answer: 1.5.
Problem 21.
In triangle ABC, angle C is equal to 90 CH – height, AB = 2, Find AH.
Solution:
From ABC we find BC \u003d AB \u003d 1 (by the property of the leg lying opposite the angle 30),
then
,5.
Answer: 1.5.
Once again, what are the sine, cosine and tangent of an angle in a right triangle.
How to remember these ratios? The best way is to solve many problems, both in geometry lessons and in preparation for the exam. Then all formulas, equalities, ratios will be remembered by themselves.
We looked at problems for solving right triangles – that is, for finding unknown sides or angles. But that’s not all! In the variants of the exam in mathematics, there are many tasks where the sine, cosine, tangent or cotangent of the outer angle of the triangle appears. More on this in the next article.
If you liked the analysis of this topic, sign up for online USE preparation courses in mathematics
Thank you for using our publications.
The information on the page “Sine, cosine and tangent of an acute angle of a right triangle” was prepared by our editors specifically to help you master the subject and prepare for exams.


 Nasal secretions need treatment with nasal saline when they block the nose. Also, treat if they make breathing through the nose hard. If breathing is noisy, it may mean the dried mucus is farther back. Nasal saline rinses can remove it.
Nasal secretions need treatment with nasal saline when they block the nose. Also, treat if they make breathing through the nose hard. If breathing is noisy, it may mean the dried mucus is farther back. Nasal saline rinses can remove it. Pain occurs mainly behind the cheekbone or eye or
Pain occurs mainly behind the cheekbone or eye or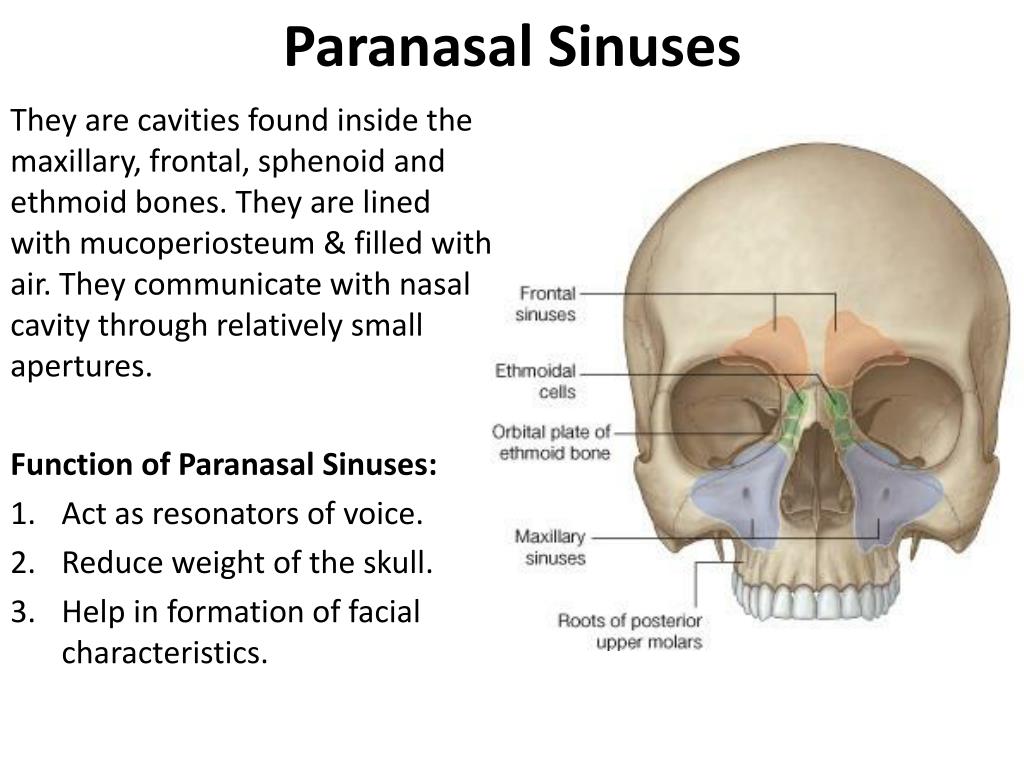 Exception: yellow or green tinged secretions are normal.
Exception: yellow or green tinged secretions are normal.
 Then, do the other side.
Then, do the other side.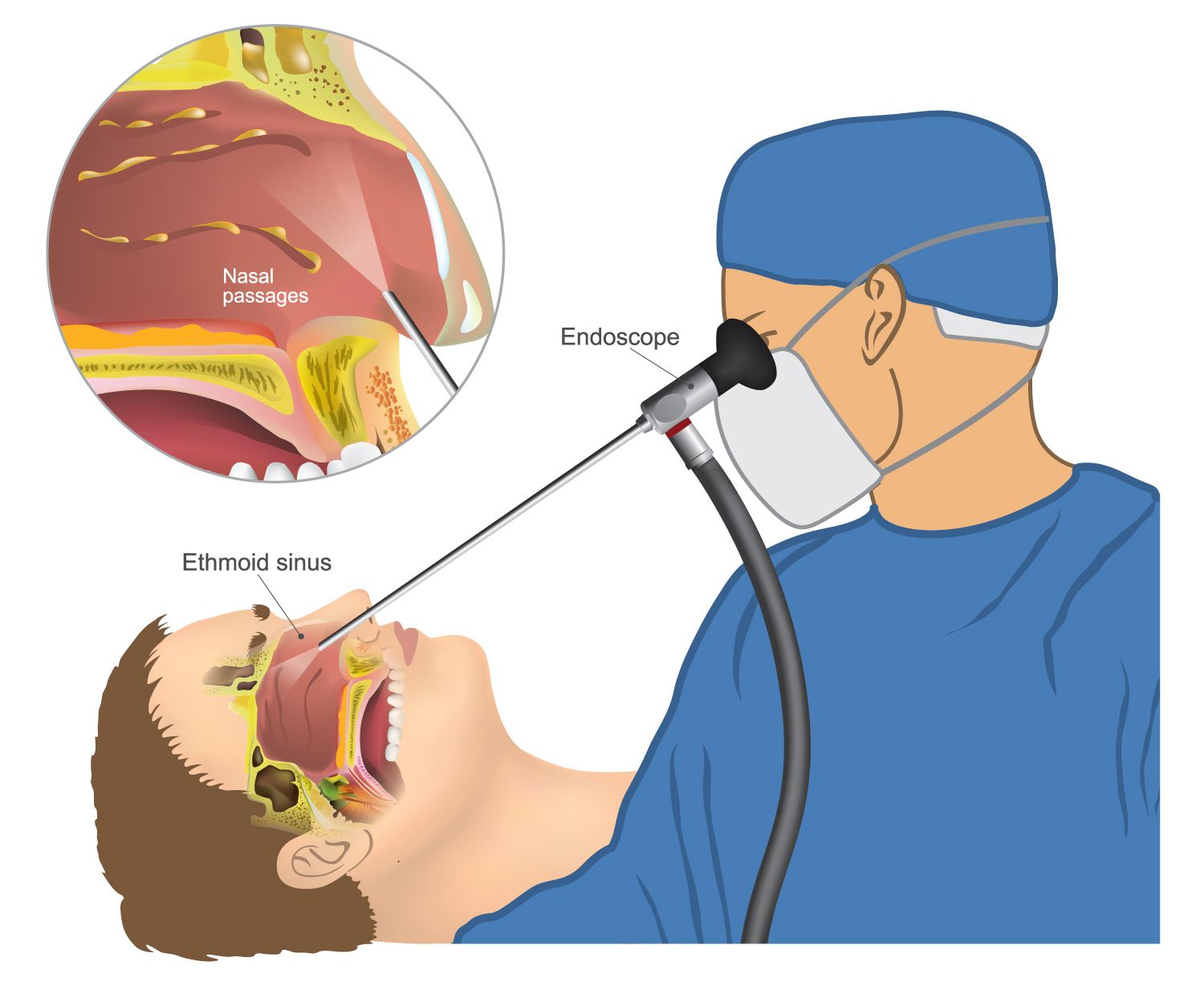 Use the long-acting type (such as Afrin).
Use the long-acting type (such as Afrin).

 Likewise,
Likewise,