Ast score. AST to Platelet Ratio Index (APRI): A Simple Tool for Assessing Liver Fibrosis
What is the AST to Platelet Ratio Index (APRI). How is APRI calculated and interpreted. What are the advantages and limitations of using APRI. How does APRI compare to other non-invasive fibrosis tests. When should clinicians consider using APRI in practice.
Understanding the AST to Platelet Ratio Index (APRI)
The AST to Platelet Ratio Index, commonly known as APRI, is a simple non-invasive tool used to assess liver fibrosis and cirrhosis. Developed by Dr. Anna S. Lok and colleagues, APRI was created to provide a cost-effective and widely accessible method for estimating liver disease severity, particularly in resource-limited settings.
APRI utilizes two routine laboratory tests:
- Aspartate aminotransferase (AST) level
- Platelet count
By combining these two parameters, APRI can provide valuable insights into the progression of liver fibrosis without the need for more invasive or expensive diagnostic procedures.
How is APRI calculated?
The APRI score is calculated using the following formula:
APRI = [(AST / upper limit of normal AST) x 100] / platelet count (10^9/L)
This simple calculation can be performed quickly, making it an attractive option for busy clinical settings.
Interpreting APRI Results: Understanding Liver Fibrosis Severity
Interpreting APRI results requires understanding the cutoff values associated with different stages of liver fibrosis. While there is some variation in the literature, generally accepted cutoffs include:
- APRI < 0.5: Low probability of significant fibrosis
- APRI 0.5-1.5: Indeterminate
- APRI > 1.5: Suggestive of significant fibrosis or cirrhosis
It’s important to note that these cutoffs may vary depending on the underlying liver disease and specific clinical context. Clinicians should interpret APRI results in conjunction with other clinical and laboratory findings.
What is the negative predictive value of APRI?
APRI has a better negative predictive value than positive predictive value. This means that a low APRI score is more reliable in ruling out cirrhosis than a high APRI score is in confirming its presence. Dr. Lok emphasizes that APRI is not very sensitive in identifying cirrhosis, but it can be useful in excluding advanced liver disease when the score is low.
Advantages of Using APRI in Clinical Practice
APRI offers several advantages that make it an attractive option for clinicians:
- Simplicity: APRI can be calculated quickly using readily available laboratory data.
- Cost-effectiveness: No additional tests or specialized equipment are required.
- Wide applicability: APRI can be used in various clinical settings, including resource-limited areas.
- Non-invasive: Unlike liver biopsy, APRI does not carry risks associated with invasive procedures.
- Repeatability: APRI can be easily repeated to monitor disease progression over time.
These advantages make APRI a valuable tool for initial assessment and ongoing monitoring of liver fibrosis, particularly in settings where more advanced diagnostic techniques may not be available.
Limitations and Considerations When Using APRI
While APRI is a useful tool, it’s essential to understand its limitations:
- Lack of specificity: APRI may be influenced by factors other than liver fibrosis, such as acute hepatitis or medication-induced liver injury.
- Indeterminate range: A significant proportion of patients may fall into the indeterminate range, requiring additional testing.
- Variable performance: The accuracy of APRI may vary depending on the underlying liver disease etiology.
- Limited sensitivity for early fibrosis: APRI may not accurately detect mild to moderate fibrosis.
Dr. Lok emphasizes that APRI should be viewed as an estimation tool rather than a definitive diagnostic test. When APRI results are discordant with other clinical data, clinicians should consider repeating the assessment during follow-up and take into account all available evidence.
How does APRI compare to other non-invasive fibrosis tests?
APRI is one of several non-invasive tests available for assessing liver fibrosis. While it offers advantages in terms of simplicity and cost-effectiveness, other tests may provide additional information or improved accuracy in certain situations:
- FibroTest/FibroSure: A proprietary algorithm using multiple serum biomarkers
- FIB-4: Combines age, AST, ALT, and platelet count
- Transient elastography (FibroScan): Measures liver stiffness using ultrasound-based technology
- Magnetic resonance elastography: Provides detailed liver stiffness measurements using MRI
The choice of fibrosis assessment tool should be based on the specific clinical scenario, available resources, and individual patient factors.
Clinical Applications: When to Consider Using APRI
APRI can be a valuable tool in various clinical scenarios:
- Initial assessment of liver fibrosis in patients with chronic liver diseases
- Monitoring disease progression in patients with known liver fibrosis
- Screening for advanced fibrosis in high-risk populations
- Prioritizing patients for further diagnostic evaluation or treatment
- Assessing liver disease severity in resource-limited settings
Dr. Lok provides an example of how she uses APRI in her clinical practice: “If I see a patient in clinic with no biopsy, no decompensation, no imaging, no elastography, I can estimate in my head APRI as long as I have AST and platelet count, and can make a good estimate of the stage of liver disease.”

How can APRI guide clinical decision-making?
APRI results can inform several aspects of patient care:
- Treatment urgency: Higher APRI scores may indicate a need for more aggressive treatment approaches.
- Cirrhosis care: Elevated APRI scores can prompt initiation of cirrhosis-specific management, such as hepatocellular carcinoma surveillance.
- Follow-up planning: APRI can help determine the frequency and intensity of patient monitoring.
- Resource allocation: In settings with limited access to specialized care, APRI can help prioritize patients for referral to hepatology specialists.
APRI in the Context of Viral Hepatitis Management
APRI has been particularly well-studied in the context of viral hepatitis, especially hepatitis B and C. With the advent of direct-acting antivirals (DAAs) for hepatitis C, the role of fibrosis assessment tools like APRI has evolved.
How has the availability of DAAs impacted the use of APRI in hepatitis C management?
The widespread availability of highly effective DAAs has changed the landscape of hepatitis C treatment. While fibrosis assessment remains important for prognostication and post-treatment monitoring, the threshold for treatment initiation has lowered significantly. Dr. Lok notes that while we cannot eradicate hepatitis C without a vaccine, we can work towards elimination by identifying and treating all infected individuals.

In this context, APRI can still play a role in:
- Prioritizing patients for treatment in resource-limited settings
- Identifying patients who may require closer monitoring during and after treatment
- Assessing the risk of liver-related complications in patients with a history of hepatitis C
Future Directions: Enhancing Liver Fibrosis Assessment
While APRI remains a valuable tool, ongoing research aims to improve non-invasive fibrosis assessment methods. Some areas of active investigation include:
- Combination algorithms: Integrating multiple non-invasive markers to improve diagnostic accuracy
- Machine learning approaches: Utilizing artificial intelligence to analyze complex data patterns
- Novel biomarkers: Identifying new serum or imaging markers specific to liver fibrosis
- Point-of-care testing: Developing rapid, bedside tests for fibrosis assessment
Dr. Lok’s research group is particularly excited about prospects for hepatitis B cure, which could significantly impact the landscape of chronic liver disease management.

What role might APRI play in future liver disease management strategies?
As our understanding of liver disease evolves and new treatments become available, APRI is likely to remain relevant due to its simplicity and wide applicability. However, its role may shift towards:
- Initial screening in primary care settings
- Monitoring treatment response in conjunction with other markers
- Risk stratification in population health management programs
- Longitudinal assessment of liver health in patients with multiple risk factors
The integration of APRI with other clinical data and emerging biomarkers may enhance its utility in personalized liver disease management strategies.
Optimizing APRI Usage: Tips for Clinicians
To maximize the benefits of APRI in clinical practice, consider the following tips:
- Understand the context: Interpret APRI results in light of the patient’s overall clinical picture and risk factors.
- Use serial measurements: Tracking APRI over time can provide valuable insights into disease progression or treatment response.
- Combine with other tools: When possible, use APRI in conjunction with other non-invasive fibrosis assessment methods for improved accuracy.
- Educate patients: Help patients understand the meaning of their APRI score and its implications for their liver health.
- Stay updated: Keep abreast of new research and guidelines regarding APRI interpretation and application.
By following these recommendations, clinicians can harness the full potential of APRI as a simple yet powerful tool in liver disease management.
How can clinicians effectively communicate APRI results to patients?
When discussing APRI results with patients, consider the following approaches:
- Use simple language to explain the concept of liver fibrosis and its progression
- Provide context for the APRI score, emphasizing that it is an estimate rather than a definitive diagnosis
- Discuss the implications of the APRI result for the patient’s overall liver health and management plan
- Address any patient concerns or misconceptions about liver disease and fibrosis assessment
- Emphasize the importance of lifestyle modifications and adherence to treatment plans, regardless of the APRI score
Clear communication about APRI results can help patients better understand their liver health status and engage more actively in their care.
AST to Platelet Ratio Index (APRI)
Dr. Anna S. Lok
From the Creator
Why did you develop the APRI? Was there a particular clinical experience or patient encounter that inspired you to create this tool for clinicians?
We developed the APRI to find a simple, no cost method to estimate liver fibrosis and cirrhosis severity that can be applied in any part of the world.
What pearls, pitfalls and/or tips do you have for users of the APRI? Do you know of cases when it has been applied, interpreted, or used inappropriately?
APRI provides an estimation. It is not gospel, and users need to understand the limitations. For example, when the APRI result is discordant from other clinical data, one should consider repeating the assessment again during follow up, and take into account all available evidence. APRI has better negative predictive value than positive predictive value, i. e., low APRI is reliable in ruling out cirrhosis, but APRI is not very sensitive in identifying cirrhosis.
e., low APRI is reliable in ruling out cirrhosis, but APRI is not very sensitive in identifying cirrhosis.
What recommendations do you have for doctors once they have applied the APRI? Are there any adjustments or updates you would make to the score based on new data or practice changes?
Knowing whether patients have advanced fibrosis or cirrhosis can determine urgency of treatment and need for cirrhosis care, e.g. HCC surveillance.
How do you use the APRI in your own clinical practice? Can you give an example of a scenario in which you use it?
If I see a patient in clinic with no biopsy, no decompensation, no imaging, no elastography, I can estimate in my head APRI as long as I have AST and platelet count, and can make good estimate of the stage of liver disease.
With the advent of and increasing access to DAAs for hepatitis C, how close are we to eradicating the disease?
We cannot eradicate hepatitis C until we have a vaccine, but we can eliminate it if we are able to find everyone who is infected and get them started on treatment.
Any research you have in the pipeline that you’re particularly excited about?
Prospects for HBV cure.
About the Creator
Anna S. Lok, MD, FAASLD, is a hepatology research professor and assistant dean for clinical research in the internal medicine department at the University of Michigan. She is also director of clinical hepatology at the University of Michigan Health System and the immediate past-president of the American Association for the Study of Liver Diseases. Dr. Lok’s research focuses primarily on the history and treatment of hepatitis B and C, hepatocellular carcinoma, and nonalcoholic fatty liver disease.
To view Dr. Anna S. Lok’s publications, visit PubMed
Diagnostic accuracy of FibroScan-AST (FAST) score for the non-invasive identification of patients with fibrotic non-alcoholic steatohepatitis: a systematic review and meta-analysis
Article Text
Article menu
- Article
Text - Article
info - Citation
Tools - Share
- Rapid Responses
- Article
metrics - Alerts
Hepatology
Original research
Diagnostic accuracy of FibroScan-AST (FAST) score for the non-invasive identification of patients with fibrotic non-alcoholic steatohepatitis: a systematic review and meta-analysis
- http://orcid.
 org/0000-0002-1142-8585Federico Ravaioli1,2,3,
org/0000-0002-1142-8585Federico Ravaioli1,2,3, - Elton Dajti2,3,
- Alessandro Mantovani4,
- http://orcid.org/0000-0001-6085-3652Philip Noel Newsome5,6,
- http://orcid.org/0000-0002-4325-3900Giovanni Targher4,
- http://orcid.org/0000-0002-8384-801XAntonio Colecchia1
- 1
Gastroenterology Unit, Department of Medical Specialities, University Hospital of Modena, University of Modena & Reggio Emilia, Modena, Italy
- 2
Department of Medical and Surgical Sciences (DIMEC), University of Bologna, Bologna, Italy
- 3
IRCCS Azienda Ospedaliero-Universitaria di Bologna, Bologna, Italy
- 4
Section of Endocrinology, Diabetes and Metabolism, Department of Medicine, University and Azienda Ospedaliera Universitaria Integrata of Verona, Verona, Italy
- 5
National Institute for Health Research, Birmingham Biomedical Research Centre at University Hospitals Birmingham NHS Foundation Trust, Birmingham, UK
- 6
Centre for Liver & Gastrointestinal Research, Institute of Immunology and Immunotherapy, University of Birmingham, Birmingham, UK
- Correspondence to
Professor Antonio Colecchia, Department of Medical Specialities, University of Modena and Reggio Emilia, Modena, 41121, Italy; antonio. colecchia{at}unimore.it
colecchia{at}unimore.it
Abstract
Objective A simple combined score with liver stiffness, controlled attenuation parameter and serum aspartate aminotransferase (AST), the FibroScan-AST (FAST) score, has been proposed to non-invasively identify patients with fibrotic non-alcoholic steatohepatitis (NASH). We performed a systematic review and meta-analysis of published studies to evaluate the overall diagnostic accuracy of the FAST score in identifying patients with fibrotic NASH.
Design We systematically searched MEDLINE, Ovid Embase, Scopus and Cochrane Library electronic databases for full-text published articles in any language between 3 February 2020 and 30 April 2022. We included original articles that reported data for the calculation of sensitivity and specificity of the FAST score for identifying adult patients with fibrotic NASH adults, according to previously described rule-out (≤0.35) and rule-in (≥0.67) cut-offs.
Results We included 12 observational studies for a total of 5835 participants with biopsy-confirmed non-alcoholic fatty liver disease. The pooled prevalence of fibrotic NASH was 28% (95% CI 21% to 34%). The FAST score’s pooled sensitivity was 89% (95% CI 82% to 93%), and the pooled specificity was 89% (95% CI 83% to 94%) according to the aforementioned rule-in/rule-out cut-offs. The negative predictive value and positive predictive value of the FAST score were 92% (95% CI 91% to 95%) and 65% (95% CI 53% to 68%), respectively. Subgroup analyses and influential bias analyses did not alter these findings.
The pooled prevalence of fibrotic NASH was 28% (95% CI 21% to 34%). The FAST score’s pooled sensitivity was 89% (95% CI 82% to 93%), and the pooled specificity was 89% (95% CI 83% to 94%) according to the aforementioned rule-in/rule-out cut-offs. The negative predictive value and positive predictive value of the FAST score were 92% (95% CI 91% to 95%) and 65% (95% CI 53% to 68%), respectively. Subgroup analyses and influential bias analyses did not alter these findings.
Conclusion The results of our meta-analysis show that the FAST score has a good performance for non-invasive diagnosis of fibrotic NASH. Therefore, this score can be used to efficiently identify patients who should be referred for a conclusive liver biopsy and/or consideration for treatment with emerging pharmacotherapies.
PROSPERO registration number CRD42022350945.
- NONALCOHOLIC STEATOHEPATITIS
- LIVER IMAGING
- FATTY LIVER
- ULTRASONOGRAPHY
- HEPATIC FIBROSIS
Data availability statement
All data relevant to the study are included in the article or uploaded as online supplemental information. The full search strategy and key results used to generate data that inform the conclusions of this systematic review can be found in online supplemental material.
The full search strategy and key results used to generate data that inform the conclusions of this systematic review can be found in online supplemental material.
http://dx.doi.org/10.1136/gutjnl-2022-328689
Statistics from Altmetric.com
Request Permissions
If you wish to reuse any or all of this article please use the link below which will take you to the Copyright Clearance Center’s RightsLink service. You will be able to get a quick price and instant permission to reuse the content in many different ways.
- NONALCOHOLIC STEATOHEPATITIS
- LIVER IMAGING
- FATTY LIVER
- ULTRASONOGRAPHY
- HEPATIC FIBROSIS
Data availability statement
All data relevant to the study are included in the article or uploaded as online supplemental information. The full search strategy and key results used to generate data that inform the conclusions of this systematic review can be found in online supplemental material.
View Full Text
Footnotes
FR and ED are joint first authors.

GT and AC are joint senior authors.
Twitter @FedRavaioli, @EltonDajti, @phil_newsome7, @antoniocolecch4
FR and ED contributed equally.
Contributors FR, ED, AM, GT and AC formulated the research questions and developed the study protocol. FR, ED and AM collected and extracted the data, with GT and AC providing supervision and guarantors of the study. FR, ED, and AM analysed the data. FR, ED, AM, PNN, GT and AC wrote the manuscript. All authors had full access to all the data in the study, reviewed the manuscript, and had final responsibility for the decision to submit for publication.
Funding The authors have not declared a specific grant for this research from any funding agency in the public, commercial or not-for-profit sectors.
Competing interests None declared.
Patient and public involvement Patients and/or the public were not involved in the design, or conduct, or reporting, or dissemination plans of this research.

Provenance and peer review Not commissioned; externally peer reviewed.
Supplemental material This content has been supplied by the author(s). It has not been vetted by BMJ Publishing Group Limited (BMJ) and may not have been peer-reviewed. Any opinions or recommendations discussed are solely those of the author(s) and are not endorsed by BMJ. BMJ disclaims all liability and responsibility arising from any reliance placed on the content. Where the content includes any translated material, BMJ does not warrant the accuracy and reliability of the translations (including but not limited to local regulations, clinical guidelines, terminology, drug names and drug dosages), and is not responsible for any error and/or omissions arising from translation and adaptation or otherwise.
Read the full text or download the PDF:
Subscribe
Log in using your username and password
For personal accounts OR managers of institutional accounts
Username *
Password *
Forgot your log in details?Register a new account?
Forgot your user name or password?
Read the full text or download the PDF:
Subscribe
Log in using your username and password
For personal accounts OR managers of institutional accounts
Username *
Password *
Forgot your log in details?Register a new account?
Forgot your user name or password?
Methods of quick counting without a calculator
Numbers surround us since childhood. Even before school or in the first grade, a person learns to add and subtract, to solve simple examples and problems. Later, he masters the multiplication table, moving on to the more difficult part of the math exercises. Most people can only do simple calculations in their minds. But multiplication and division of large values \u200b\u200bhas to be performed on paper or using a calculator. But is it possible to somehow learn to count well without using improvised means?
Even before school or in the first grade, a person learns to add and subtract, to solve simple examples and problems. Later, he masters the multiplication table, moving on to the more difficult part of the math exercises. Most people can only do simple calculations in their minds. But multiplication and division of large values \u200b\u200bhas to be performed on paper or using a calculator. But is it possible to somehow learn to count well without using improvised means?
Quick calculation without a calculator
The life of any modern person is inextricably linked with numbers. Without the ability to count, it is impossible to perform the most simple everyday tasks. Of course, today people have smart assistants – calculators, smartphones, computers, but even they can sometimes fail – break down or run out of power at the wrong time. And it’s not always possible to rely on gadgets, because they won’t help you in exams at school or at a university. That is why many people strive to learn how to count well without the help of improvised means. This is especially true for schoolchildren, because if you master the techniques of fast mental counting from childhood, then both studying at school and various tasks in adulthood will be easier.
This is especially true for schoolchildren, because if you master the techniques of fast mental counting from childhood, then both studying at school and various tasks in adulthood will be easier.
There is another good reason to start practicing mental counting well. Mental counting develops the human brain and contributes to the growth of the level of intelligence. Therefore, even those students who study in the humanities still study such exact sciences as higher mathematics and mathematical analysis. Exercises aimed at mental counting of large numbers are an excellent exercise for the mind. So the development of intelligence and convenience in everyday life are the two most important reasons to learn how to count well without a calculator.
Mankind has been striving since ancient times to find such ways of fast counting. And we are talking not only about simple calculations, such as addition and subtraction, but also about more complex ones, such as multiplication and division. Although it takes a lot of time, you can still add and subtract large values without prior preparation, but such actions as multiplying two-digit numbers are not available to most people.
Although it takes a lot of time, you can still add and subtract large values without prior preparation, but such actions as multiplying two-digit numbers are not available to most people.
But, thanks to the work of mathematicians from all over the globe, today some mathematical tricks have appeared that allow you to count in your mind not only single-digit, but also double-digit numbers. To understand the principle of their work, it is better to consider each of these techniques separately.
Popular quick counting system
There are several types of basic mathematical operations – addition, subtraction, multiplication and division. And if everything is more or less clear with finding the sum and difference, then other calculations are much more difficult to perform. Consider the most popular mathematical tricks aimed at convenient multiplication and division in the mind.
Multiplication of any number by 9
Solving such examples orally is very easy. To do this, just multiply the desired value by 10 and subtract the same number from the resulting answer. For example, we need to find the result of multiplying 19and 9. The example would look like this: 19*10-19= 190-19=171. This approach is quite easy to apply in practice.
To do this, just multiply the desired value by 10 and subtract the same number from the resulting answer. For example, we need to find the result of multiplying 19and 9. The example would look like this: 19*10-19= 190-19=171. This approach is quite easy to apply in practice.
Multiplying any number by 11
Multiplying any value by 11 looks similar: we find the product of our number and 10, and then add our number to the resulting expression. Let’s say we are looking for how much 67*11 will be, so we get the following example: 67*10+67=670+67=737.
Multiplying a two-digit number by a single-digit number
The easiest way to perform such an operation is by parsing multipliers into tens and ones. Let’s say we need to multiply 56 and 8. To do this, we divide 56 into its component parts, it turns out 50 and 6. Now we separately multiply our tens and ones by a single digit and look for their sum. It turns out 50*8+6*8=400+48=448. But the more characters in each of the multiplied values, the more difficult it is to perform such operations in the mind.
Multiplying a two-digit number by a two-digit number
Finding the result of multiplying two-digit numbers is similar to the previous method. For example, you need to find the product of 24 and 52. To do this, we divide one of the numbers into tens and ones and multiply them by our factor, and then add the resulting expressions: 20*52+4*52=1040+208=1248. The larger each of the numbers, the more difficult it is to find the result of multiplication.
Finding the percentage of a number
To find the percentage of any value, you need to multiply this number by the size of the desired percentage and divide by one hundred. It is better to consider this approach with an example. Let’s say we want to find 12% of 74. We multiply 12 and 74, parsing this expression into its component parts. It turns out 10*74+2*74=740+148=888. Now we divide our result by 100 and get the answer – 8.88%. This makes it easy to find the percentage of any value without the help of a calculator.
Dividing a multidigit number by a single digit
To find the answer to this example, you need to remember the multiplication table. Let’s say we need to divide the number 138 by 6. To do this, we divide the dividend into parts, we get 13 tens and 8 units. We divide 13 by 6, we get 2 and 1 in the remainder. This means that the ten in our answer will be the number 2. The remainder, and this is 1 ten, we add with the unit of the dividend, it turns out 18. We divide 18 by 6, it turns out 3. Now we add the resulting tens and ones: 20 + 3 \u003d 23. The whole expression will look like this: 120/6+(10+8)/6=20+18/6=23.
There are other, more sophisticated methods of verbal mathematical calculations that allow you to perform operations with multi-digit numbers. But these techniques are also more difficult to master, as they require high concentration and a well-developed memory.
One of the advantages of all such tricks is the fact that such an account can be learned fairly quickly. The listed methods have many variations from simple to more complex, so even children are willing to use some of them. But all these methods have one significant drawback, which does not allow them to be called a full-fledged mental counting system.
The listed methods have many variations from simple to more complex, so even children are willing to use some of them. But all these methods have one significant drawback, which does not allow them to be called a full-fledged mental counting system.
Such methods of calculation imply the fulfillment of a number of conditions. For example, the rules for multiplying three-digit numbers are different from those for two-digit numbers. Therefore, it is necessary to memorize a large number of conditions so that such counting methods can be used in everyday life. All this makes such methods of addition, subtraction, multiplication and division more of an exercise for the mind than a productive approach to calculations.
But there are also radically different techniques that allow you to develop a person’s skills and learn to count very well without improvised means. One of the most popular methods of fast mental counting is mental arithmetic. Let’s consider its advantages in more detail.
How to teach a child to count mentally
Mental arithmetic is far from a new system of quick counting, because it originated in antiquity, about five thousand years ago. Since then, this technique has not undergone major changes and has come down to us in almost its original form. It is based on calculations on the abacus – special accounts. First, a person learns to solve the simplest examples on them, and then gradually moves on to a more complex stage of learning – he learns to imagine an abacus in his mind and make calculations on it in his imagination.
Mental arithmetic is best for children. No, adults can also master it, but for this they will have to abstract from the usual methods of operations with numbers, and the child copes with this much easier. For him, mental arithmetic is not only an assistant in mathematics lessons, but also a way to develop his intellectual abilities to a very high level.
The whole secret of this technique is that it implies the versatile development of a person. The right hemisphere of the brain is responsible for logic and analysis, it is it that is involved in ordinary math lessons when we solve examples or problems. The right hemisphere, which is responsible for creative thinking and fantasy, in this case is almost not connected to work, and therefore does not develop properly. But all areas of the human intellect need to be trained.
The right hemisphere of the brain is responsible for logic and analysis, it is it that is involved in ordinary math lessons when we solve examples or problems. The right hemisphere, which is responsible for creative thinking and fantasy, in this case is almost not connected to work, and therefore does not develop properly. But all areas of the human intellect need to be trained.
Since mental arithmetic involves both analytical thinking and imagination, it is not so much a way to quickly solve mathematical problems as a means for comprehensive development. Other techniques are most often aimed at training a single ability, and this technique works in a complex way. This is what distinguishes it from others and makes it one of the most popular systems for developing the child’s intellect.
Learning mental arithmetic takes a lot of time, but the benefits it gives are worth the effort. When it comes to teaching a child according to this technique, it is important to choose the right training program. A key success factor is adherence to the lesson plan and control of their regularity. Despite the fact that in open sources on the Internet you can find a lot of information on this request, it is not always possible to master mental arithmetic on your own. Therefore, most parents prefer to teach their child this technique in children’s centers for additional education.
A key success factor is adherence to the lesson plan and control of their regularity. Despite the fact that in open sources on the Internet you can find a lot of information on this request, it is not always possible to master mental arithmetic on your own. Therefore, most parents prefer to teach their child this technique in children’s centers for additional education.
How to choose an effective method
Today, many educational institutions offer courses in mental arithmetic. But children’s education is a very complex and multifaceted process, so parents should approach it carefully and choose activities that will definitely benefit.
When choosing a school of mental arithmetic, pay attention to the fact that the training is conducted according to a proven methodology and takes into account the age characteristics of each child. It is impossible for children from elementary school and high school students to study in the same group, because each age has its own speed of mastering, memorizing and consolidating the material.
In addition, young children are best taught any subject in a playful way. So they will not get tired of studying and will be able to maintain concentration throughout the lesson. The introduction of the game into the educational process helps to increase the child’s interest in mathematics.
It is very important that the trainer has time to pay attention to each student during the session, but this is only possible in small groups. Therefore, it is worth giving preference to those children’s centers where the teacher teaches no more than ten children at a time. Only then will it be possible to engage in maximum productivity.
If the curriculum is organized correctly, then the child will be able to acquire useful skills, thanks to which mathematics will become an interesting and favorite subject for him. All this will positively affect school performance, because when studying is easy, it is much more fun to study.
All this makes learning mental arithmetic the most productive way to learn fast mental counting. The child will no longer have to resort to various mathematical tricks to easily cope with problems and examples. The student acquires skills that remain for life, which means they will be useful to him not only in his studies, but also in his career. All this makes learning this technique an excellent investment in the future of your child.
The child will no longer have to resort to various mathematical tricks to easily cope with problems and examples. The student acquires skills that remain for life, which means they will be useful to him not only in his studies, but also in his career. All this makes learning this technique an excellent investment in the future of your child.
Methods of mental counting for quick calculation in the mind
Why count in the mind, if you can solve any arithmetic problem on a calculator. Modern medicine and psychology prove that mental counting is an exercise for gray cells. Performing such gymnastics is necessary for the development of memory and mathematical abilities.
There are many ways to simplify mental calculations. Everyone who has seen the famous painting by Bogdanov-Belsky “Mental Account” is always surprised – how do peasant children solve such a difficult task as dividing the sum of five numbers that must first be squared?
It turns out that these children are students of the famous teacher-mathematician Sergei Alexandrovich Rachitsky (he is also depicted in the picture). These are not child prodigies – elementary school students of a nineteenth-century village school. But they all already know how to simplify arithmetic calculations and have learned the multiplication table! Therefore, it is quite possible for these kids to solve such a problem!
These are not child prodigies – elementary school students of a nineteenth-century village school. But they all already know how to simplify arithmetic calculations and have learned the multiplication table! Therefore, it is quite possible for these kids to solve such a problem!
Secrets of mental counting
There are tricks of mental counting – simple algorithms that it is desirable to bring to automatism. After mastering simple techniques, you can move on to mastering more complex ones.
Adding the numbers 7,8,9
To simplify the calculations, the numbers 7,8,9 must first be rounded up to 10, and then subtract the increase. For example, to add 9 to a two-digit number, you must first add 10 and then subtract 1, and so on.
Examples :
56+7=56+10-3=63 82
Fast add two-digit numbers
If the last digit of a two-digit number is greater than five, round it up. We perform the addition, subtract the “additive” from the resulting amount.
Examples :
54+39=54+40-1=93
put in ranks: first add tens, then units.
Example :
57+32=57+30+2=89
0002 32+57 \u003d 32 + 60-3 \u003d 89
Add three-digit numbers in your head
Quick counting and addition of three-digit numbers – is it possible? Yes. To do this, you need to parse three-digit numbers into hundreds, tens, units and add them one by one.
Example :
249+533=(200+500)+(40+30)+(9+3)=782
Subtraction features: reduction to round numbers
Subtracted are rounded up to 10, up to 100. If you need to subtract a two-digit number, you need to round it up to 100, subtract it, and then add an amendment to the remainder. This is true if the correction is small.
Examples :
If at one time it was well learned composition of numbers from 1 to 10, then the subtraction can be done in parts and in the specified order: hundreds, tens, units.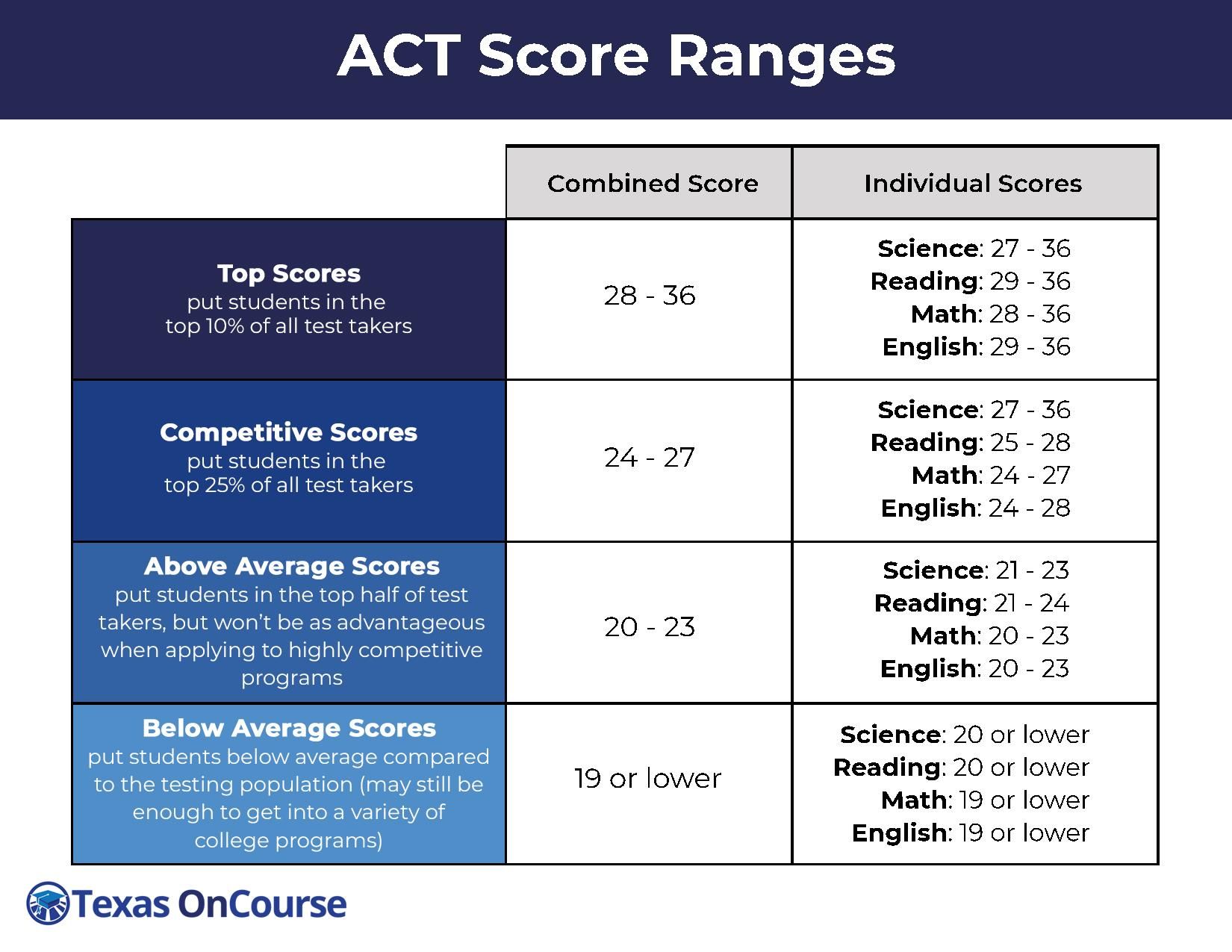
Example :
843-596=843-500-90-6=343-90-6=253-6=247
mentally multiply and divide in the mind? It is possible, but one cannot do without knowledge of the multiplication table. The multiplication table is the golden key to quick mental counting! It applies to both multiplication and division. Recall that in the elementary grades of a village school in the pre-revolutionary Smolensk province (the painting “Mental Counting”), children knew the continuation of the multiplication table – from 11 to 19!
Although in my opinion it is enough to know the table from 1 to 10 in order to be able to multiply larger numbers. For example :
15*16=15*10+(10*6+5*6)=150+60+30=240
02 Mastering multiplication table by 2 and by 3 to automatism, making the rest of the calculations will be as easy as shelling pears.
For multiplication and division of two- and three-digit numbers, we use simple tricks:
times 4 is twice times 2;
multiply by 6 – this means multiply by 2, and then by 3;
multiplied by 8 is three times multiplied by 2;
times 9 is twice times 3.

For example :
37*4=(37*2)*2=74*2=148;
412*6=(412*2) 3=824 3=2472
Similarly:
divided by 4 is twice divided by 2;
divided by 6 is first divided by 2 and then by 3;
divided by 8 is three times divided by 2;
divided by 9 is twice divided by 3.
For example :
412:4=(412:2):2=206:2=1030003
How to multiply and divide by 5
The number 5 is half of 10 (10:2). Therefore, we first multiply by 10, then we divide the result in half.
Example :
326*5=(326*10):2=3260:2=1630 0003
326:5=(326 2):10=652:10=65.2.
Multiplying by 9
To multiply a number by 9, it is not necessary to multiply it twice by 3. It is enough to multiply it by 10 and subtract the multiplied number from the resulting number. Compare which is faster:
37*9=(37*3)*3=111*3=333
or
37*9=37*10 – 37=370-37=333
multiplication of two-digit numbers by 11 or by 101. So, when multiplied by 11, a two-digit number, as it were, moves apart. The numbers that make it up remain at the edges, and their sum is in the center. For example: 24*11=264. When multiplying by 101, it is enough to attribute the same to a two-digit number. 24*101= 2424. The simplicity and logic of such examples is admirable. Such tasks are very rare – these are entertaining examples, the so-called little tricks.
So, when multiplied by 11, a two-digit number, as it were, moves apart. The numbers that make it up remain at the edges, and their sum is in the center. For example: 24*11=264. When multiplying by 101, it is enough to attribute the same to a two-digit number. 24*101= 2424. The simplicity and logic of such examples is admirable. Such tasks are very rare – these are entertaining examples, the so-called little tricks.
Finger counting
Today you can still meet many advocates of “finger gymnastics” and the method of mental counting on fingers. We are convinced that learning to add and subtract by bending and unbending fingers is very visual and convenient. The range of such calculations is very limited. As soon as the calculations go beyond one operation, difficulties arise: it is necessary to master the next technique. Yes, and bending your fingers in the era of iPhones is somehow undignified.
For example, in defense of the “finger” technique, the method of multiplying by 9 is given. The trick is as follows:
The trick is as follows:
- To multiply any number within the first ten by 9, you need to turn your palms towards you.
- Counting from left to right, bend the finger corresponding to the multiplied number. For example, to multiply 5 by 9, you need to bend the little finger on your left hand.
- The remaining number of fingers on the left will correspond to tens, on the right – units. In our example – 4 fingers on the left and 5 on the right. Answer: 45.
Yes, indeed, the solution is quick and clear! But this is from the field of tricks. The rule only applies when multiplying by 9. Isn’t it easier to learn the multiplication table for multiplying 5 by 9? This trick will be forgotten, and a well-learned multiplication table will remain forever.
There are also many more similar tricks using fingers for some single mathematical operations, but this is relevant while you use it and is immediately forgotten when you stop using it. Therefore, it is better to learn standard algorithms that will remain for life.

 org/0000-0002-1142-8585Federico Ravaioli1,2,3,
org/0000-0002-1142-8585Federico Ravaioli1,2,3,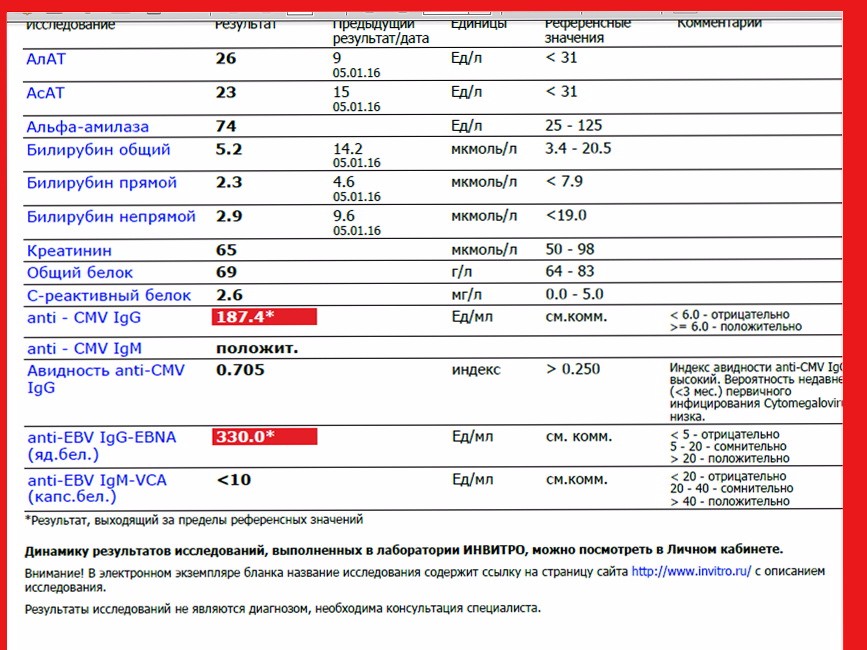 colecchia{at}unimore.it
colecchia{at}unimore.it
.gif)